题目内容
设函数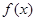 的定义域为D,若存在非零实数
的定义域为D,若存在非零实数 使得对于任意
使得对于任意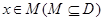 ,有
,有 ,且
,且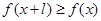 ,则称
,则称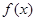 为M上的
为M上的 高调函数.
高调函数.
现给出下列命题:
① 函数 为R上的1高调函数;
为R上的1高调函数;
② 函数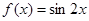 为R上的
为R上的 高调函数;
高调函数;
③ 如果定义域为 的函数
的函数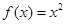 为
为 上
上 高调函数,那么实数
高调函数,那么实数 的取值范围是
的取值范围是 ;
;
④ 函数 为
为 上的2高调函数。
上的2高调函数。
其中真命题的个数为
| A.0 | B.1 | C.2 | D.3 |
D
解析试题分析:首先理解“高调函数”的定义:函数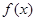 的定义域为D,若存在非零实数
的定义域为D,若存在非零实数 使得对于任意
使得对于任意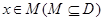 ,有
,有 ,且
,且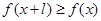 ,则称
,则称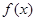 为M上的
为M上的 高调函数.
高调函数.
据此研究四个函数:
对于①,即f(x)=(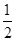 )x。f(x+l)=(
)x。f(x+l)=(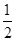 )x+l,要使f(x+l)≥f(x),需要(
)x+l,要使f(x+l)≥f(x),需要(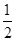 )x+l≥(
)x+l≥(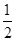 )x恒成立,只需l≤0;所以①函数
)x恒成立,只需l≤0;所以①函数 为R上的1高调函数;不对;
为R上的1高调函数;不对;
对于②,f(x+1))=sin2(x+1)≥sin2x=f(x),当l=π时恒成立;所以函数f(x)=sin2x为R上的π高调函数,
所以②对;
对于③,f(x+m)=(x+m)2,f(x)=x2,令(x+m)2≥x2,即2mx+m2≥0在 恒成立,
恒成立,
∴m>0且2m(-1)+m2≥0,解得m≥2,故③对;
对于④ 函数 ,若其为2高调函数,
,若其为2高调函数,
则由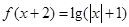 ≥
≥ ,在
,在 恒成立,
恒成立,
得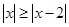 在
在 恒成立,而此恒成立,所以④对
恒成立,而此恒成立,所以④对
故正确的命题个数是3个,
故选D。
考点:本题主要考查学生的阅读能力, 常见函数的性质。
点评:新定义问题,具有较强的综合性。关键是阅读理解新定义内容,应用知识分析解决问题,利用数形结合的方法,应用图象解决问题,属中档题

 一线名师权威作业本系列答案
一线名师权威作业本系列答案“ ”是“
”是“ ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
方程 表示的图形
表示的图形
| A.是一个点 | B.是一个圆 | C.是一条直线 | D.不存在 |
已知命题 :
: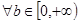 ,
,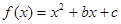 在
在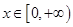 上为增函数,命题
上为增函数,命题 :
: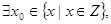 使
使 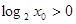 ,则下列结论成立的是( )
,则下列结论成立的是( )
A.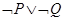 | B.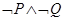 | C.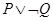 | D.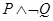 |
命题“所有实数的平方都是正数”的否定为
| A.所有实数的平方都不是正数 | B.有的实数的平方是正数 |
| C.至少有一个实数的平方是正数 | D.至少有一个实数的平方不是正数 |
已知命题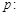 若
若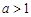 ,则
,则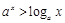 恒成立;命题
恒成立;命题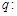 等差数列
等差数列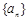 中,
中,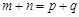 是
是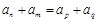 的充分不必要条件(其中
的充分不必要条件(其中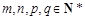 ).则下面选项中真命题是( )
).则下面选项中真命题是( )
A.(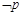 ) )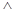 ( (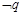 ) ) | B.(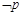 ) )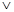 ( (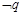 ) ) |
C.(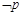 )∧ )∧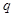 | D.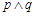 |
命题“对任意的 ,都有
,都有 ”的否定为( )
”的否定为( )
A.存在 ,使 ,使 |
B.对任意的 ,都有 ,都有 |
C.存在 ,使 ,使 |
D.存在 ,使 ,使 |
对于直线m、 n 和平面 a、b、γ,有如下四个命题:
其中正确的命题的个数是
| A.1 | B.2 | C.3 | D.4 |
已知命题 ,使得
,使得 ;
; ,使得
,使得 .以下命题为真命题的为 ( )
.以下命题为真命题的为 ( )
A. | B. | C. | D. |