题目内容
(理)数列 的前
的前 项和记为
项和记为
(Ⅰ)求 的通项公式;
的通项公式;
(Ⅱ)等差数列 的各项为正,其前
的各项为正,其前 项和为
项和为 ,且
,且 ,又
,又 成等比数列,求
成等比数列,求
 的前
的前 项和记为
项和记为
(Ⅰ)求
 的通项公式;
的通项公式;(Ⅱ)等差数列
 的各项为正,其前
的各项为正,其前 项和为
项和为 ,且
,且 ,又
,又 成等比数列,求
成等比数列,求
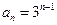 ,
,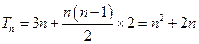
(理)解:(Ⅰ)由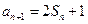 可得
可得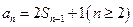 ,两式相减得
,两式相减得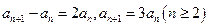
又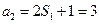 ∴
∴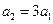
故 是首项为
是首项为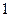 ,公比为
,公比为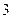 得等比数列
得等比数列
∴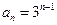
(Ⅱ)设 的公比为
的公比为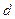
由 得,可得
得,可得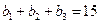 ,可得
,可得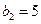
故可设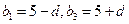
又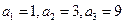
由题意可得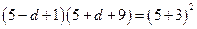
解得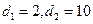
∵等差数列 的各项为正,∴
的各项为正,∴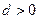
∴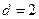
∴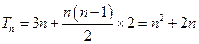
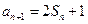 可得
可得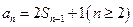 ,两式相减得
,两式相减得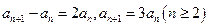
又
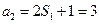 ∴
∴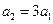
故
 是首项为
是首项为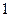 ,公比为
,公比为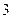 得等比数列
得等比数列∴
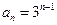
(Ⅱ)设
 的公比为
的公比为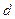
由
 得,可得
得,可得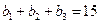 ,可得
,可得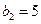
故可设
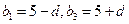
又
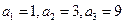
由题意可得
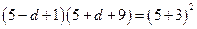
解得
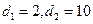
∵等差数列
 的各项为正,∴
的各项为正,∴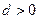
∴
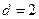
∴

练习册系列答案
相关题目
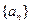 ,首项
,首项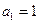 ,且对于任意
,且对于任意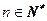 均有
均有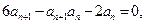
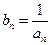
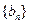 的通项公式;
的通项公式;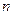 项和为
项和为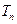 ,求证:
,求证: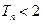 。
。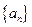 的前
的前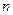 项和
项和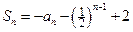 (
(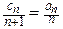 ,
,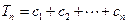 ,求
,求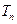 .
.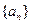 和
和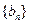 满足
满足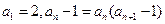 ,
,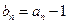 ,
,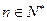 .
.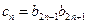 ,求使得
,求使得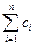
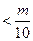 对一切
对一切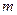 ;
;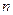 和为
和为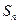 ,
,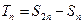 ,试比较
,试比较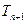 与
与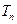 的大小.
的大小.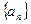 的公差大于0,且
的公差大于0,且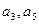 是方程
是方程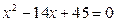 的两根,数列
的两根,数列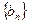 的前n项的和为
的前n项的和为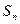 ,且
,且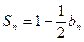 .
.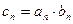 ,求证:
,求证: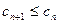 .
.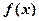 ,存在实数
,存在实数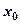 ,使得对于任意实数
,使得对于任意实数 ,总有
,总有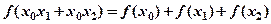 恒成立。
恒成立。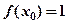 ,且对任意
,且对任意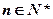 ,有
,有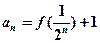 ,求{an}的通项公式;
,求{an}的通项公式;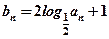 ,将数列{bn}的项重新组合成新数列
,将数列{bn}的项重新组合成新数列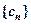 ,具体法则如下:
,具体法则如下: ,……,求证:
,……,求证: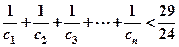 。
。 的前n项和为
的前n项和为 ,若
,若 ,
, ,则下列四个命题中真命题的序号为 ▲ .
,则下列四个命题中真命题的序号为 ▲ .  ;②
;② ;③
;③ ; ④
; ④
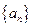 是等差数列,
是等差数列,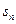 是前n项和,且
是前n项和,且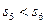 ,
,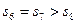 ,则下列结论错误的是
,则下列结论错误的是


 和
和 均为
均为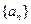 中,
中,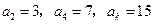 ,则
,则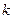 等于( ▲ )
等于( ▲ )