题目内容
2.已知各项均为正数的等比数列{an}中,a1a6=10,则lga3+lga4的值为( )| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
分析 根据等比数列的性质得到a1a6=10,得到a3a4=a1a6=10,然后把所求的式子利用对数的运算法则化简后,把求出的积代入即可求出值.
解答 解:由a1a6=10,得到a3a4=a1a6=10,
则lga3+lga4=lga3a4=lg10=1.
故选:C.
点评 此题考查学生灵活运用等比数列的性质化简求值,掌握对数的运算法则,是一道基础题.

练习册系列答案
相关题目
12.设x,y满足$\left\{\begin{array}{l}{y≥0}\\{ax+y-1≤0}\\{3x-2y-2≤0}\end{array}\right.$,若z=x2-10x+y2的最小值为-12,实数a的取值范围是( )
| A. | a$≤-\frac{1}{2}$ | B. | a$≤-\frac{3}{2}$ | C. | a$≥\frac{1}{2}$ | D. | a$<\frac{3}{2}$ |
9.若f(x)是定义在R上的奇函数,当x>0时,f(x)=$\root{3}{x+1}$,那么当x<0时,f(x)=( )
| A. | -$\root{3}{x+1}$ | B. | $\root{3}{-x+1}$ | C. | -$\root{3}{-x+1}$ | D. | $\root{3}{x-1}$ |
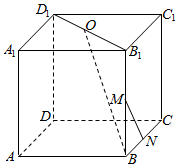 如图,正方体ABCD-A1B1C1D1中,M、N、O分别为BB1,BC,B1D1的中点,求异面直线OB与MN所成角的余弦值.
如图,正方体ABCD-A1B1C1D1中,M、N、O分别为BB1,BC,B1D1的中点,求异面直线OB与MN所成角的余弦值.