题目内容
【题目】已知圆![]() 的方程为
的方程为![]() ,直线
,直线![]() 的方程为
的方程为![]() ,点
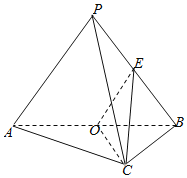
,点![]() 在直线上,过点
在直线上,过点![]() 作圆
作圆![]() 的切线
的切线![]() ,切点为
,切点为![]() .
.
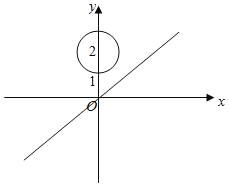
(1)若过点![]() 的坐标为
的坐标为![]() ,求切线
,求切线![]() 方程;
方程;
(2)求四边形![]() 面积的最小值;
面积的最小值;
(3)求证:经过![]() 三点的圆必过定点,并求出所有定点坐标.
三点的圆必过定点,并求出所有定点坐标.
【答案】(1)切线![]() 方程
方程![]() ,
,![]() (2)
(2)![]() (3)证明见解析;定点坐标为
(3)证明见解析;定点坐标为![]() 或
或![]()
【解析】
(1)当切线斜率不存在时,切线方程为![]() ,当切线斜率存在时,设直线方程为
,当切线斜率存在时,设直线方程为![]() ,由直线和圆相切,求出
,由直线和圆相切,求出![]() ,由此能求出切线
,由此能求出切线![]() ,
,![]() 方程.
方程.
(2)![]() ,当
,当![]() 最小时,四边形面积最小.由此能求出四边形
最小时,四边形面积最小.由此能求出四边形![]() 面积的最小值.
面积的最小值.
(3)设点![]() ,
,![]() ,过
,过![]() ,
,![]() ,
,![]() 三点的圆即以
三点的圆即以![]() 为直径的圆,由此能求出定点坐标.
为直径的圆,由此能求出定点坐标.
解:(1)当切线斜率不存在时,切线方程为![]() ,符合题意.
,符合题意.
当切线斜率存在时,设直线方程为![]() ,
,
因为直线和圆相切,所以 ,解得
,解得![]() ,
,
此时直线方程为![]() ,即
,即![]() ,
,
所以切线![]() 方程
方程![]() ,
,![]() .
.
(2)![]()
故当![]() 最小时,四边形面积最小.而
最小时,四边形面积最小.而![]()
所以四边形![]() 面积的最小值
面积的最小值![]() .
.
证明:(3)设点![]() ,
,![]() ,
,
过![]() 三点的圆即以
三点的圆即以![]() 为直径的圆
为直径的圆
即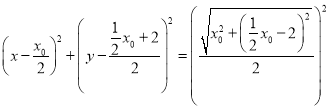 ,
,
所以![]() ,
,
从而 ,
,
解得定点坐标为![]() 或
或![]() .
.


练习册系列答案
相关题目