Question

平面内有向量=(1,7)，=(5,1)，=(2,1)，点X为直线OP上的一个动点.

(1)当·取最小值时，求的坐标；

(2)当点X满足(1)的条件和结论时，求cos∠AXB的值.

Answer 1

解：(1)设=(x,y),∵点X在直线OP上，

    ∴向量与共线.

    又=(2,1),∵x·1-y·2=0,即x=2y,∴=(2y,y).

    又=-=(1,7)-(2y,y),

    ∴=(1-2y,7-y).

    同理,=-=(5-2y,1-y).

    于是,·=(1-2y)(5-2y)+(7-y)(1-y)=4y²-12y+5+y²-8y+7=5y²-20y+12

    =5(y-2)²-8.

    由二次函数的知识，可知当y=2时，·=5(y-2)²-8有最小值-8，此时=(4,2).

    (2)当=(4,2)，即y=2时，有=(-3,5)，=(1，-1)，||=,||=,

    ·=(-3)×1+5×(-1)=-8,∴cos∠AXB===-.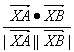

讲评：向量的坐标表示与运算可以大大简化数量积的运算，由于有关长度、角度和垂直问题可以利用向量的数量积来解决，因此，我们可以利用向量的直角坐标去研究有关长度、角度和垂直问题.