题目内容
(本小题满分12分)
设各项均为正数的数列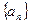 的前n项和为
的前n项和为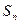 ,已知
,已知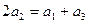 ,数列
,数列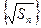 是公差为
是公差为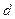 的等差数列。
的等差数列。
(1)求数列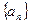 的通项公式(用
的通项公式(用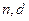 表示);
表示);
(2)设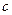 为实数,对满足
为实数,对满足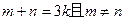 的任意正整数
的任意正整数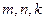 ,不等式
,不等式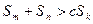 都成立。求证:
都成立。求证: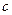 的最大值为
的最大值为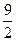 。
。
设各项均为正数的数列
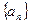 的前n项和为
的前n项和为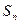 ,已知
,已知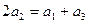 ,数列
,数列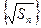 是公差为
是公差为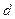 的等差数列。
的等差数列。(1)求数列
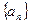 的通项公式(用
的通项公式(用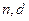 表示);
表示);(2)设
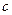 为实数,对满足
为实数,对满足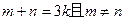 的任意正整数
的任意正整数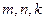 ,不等式
,不等式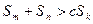 都成立。求证:
都成立。求证: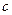 的最大值为
的最大值为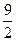 。
。(1)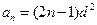
(2)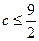 ,即
,即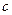 的最大值为
的最大值为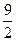 。
。
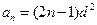
(2)
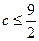 ,即
,即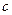 的最大值为
的最大值为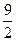 。
。解:(1)由题意知: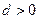 ,
, 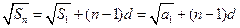
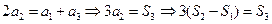 ,
,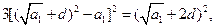
化简,得:
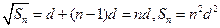 ,
,
当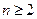 时,
时,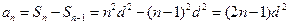 ,适合
,适合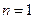 情形。
情形。
故所求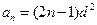
(2)
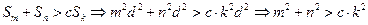 ,
, 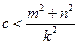 恒成立。
恒成立。
又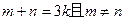 ,
,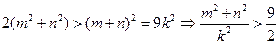 ,
,
故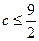 ,即
,即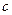 的最大值为
的最大值为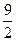 。
。
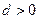 ,
, 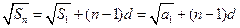
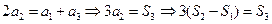 ,
,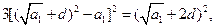
化简,得:

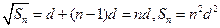 ,
,当
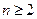 时,
时,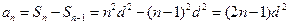 ,适合
,适合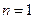 情形。
情形。故所求
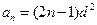
(2)
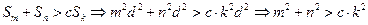 ,
, 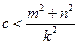 恒成立。
恒成立。又
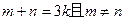 ,
,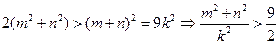 ,
,故
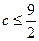 ,即
,即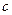 的最大值为
的最大值为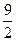 。
。
练习册系列答案
 能力评价系列答案
能力评价系列答案
相关题目
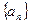 的各项均为正数,
的各项均为正数,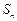 为其前
为其前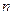 项和,对于任意
项和,对于任意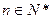 ,总有
,总有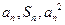 成等差数列.
成等差数列.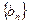 的前
的前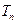 ,且
,且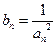 ,求证:对任意正整数
,求证:对任意正整数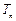
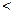 2;
2;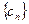 中,
中,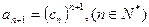 ,求数列
,求数列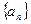 为等差数列,
为等差数列,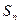 为
为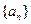 的前
的前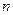 项和,已知
项和,已知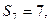
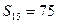 ,
,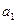 和公差
和公差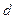 ;
; 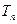 为数列
为数列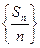 的前
的前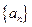 中,
中,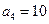 且
且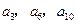 成等比数列,求数列
成等比数列,求数列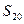 .
.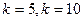 时,分别有
时,分别有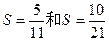
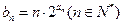 ,求数列
,求数列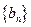 的前
的前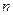 项和
项和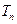 的值.
的值. 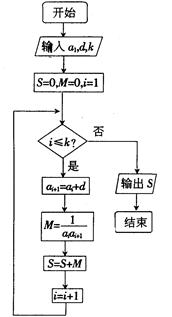
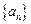 中,
中,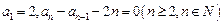 .
.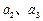 的值(只写结果)并求出数列
的值(只写结果)并求出数列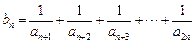 ,若对任意的正整数
,若对任意的正整数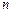 ,当
,当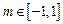 时,不等式
时,不等式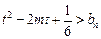 恒成立,求实数
恒成立,求实数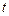 的取值范围。
的取值范围。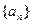 的前
的前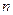 项和
项和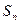 是
是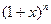 二项展开式中各项系数的和
二项展开式中各项系数的和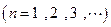 .
. 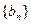 满足
满足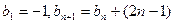 ,且
,且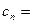
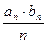 ,求数列
,求数列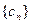 的通项及其前
的通项及其前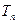 。
。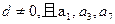 成等比数列,则
成等比数列,则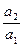 ="( " )
="( " )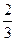
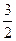
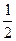
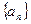 中,
中,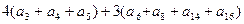 =36,那么该数列的前14项的和是 ( )
=36,那么该数列的前14项的和是 ( )