题目内容
6.设D为△ABC中BC边上的中点,且O为AD边上靠近点A的三等分点,则( )| A. | $\overrightarrow{BO}=-\frac{5}{6}\overrightarrow{AB}+\frac{1}{6}\overrightarrow{AC}$ | B. | $\overrightarrow{BO}=\frac{1}{6}\overrightarrow{AB}-\frac{1}{2}\overrightarrow{AC}$ | C. | $\overrightarrow{BO}=\frac{5}{6}\overrightarrow{AB}-\frac{1}{6}\overrightarrow{AC}$ | D. | $\overrightarrow{BO}=-\frac{1}{6}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AC}$ |
分析 可先画出图形,根据条件及向量加法、减法和数乘的几何意义即可得出
解答  解:∵D为△ABC中BC边上的中点,
解:∵D为△ABC中BC边上的中点,
∴$\overrightarrow{AD}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AC}$),
∵O为AD边上靠近点A的三等分点,
∴$\overrightarrow{OD}$=$\frac{2}{3}$$\overrightarrow{AD}$,
∴$\overrightarrow{OD}$=$\frac{1}{3}$($\overrightarrow{AB}$+$\overrightarrow{AC}$),
∴$\overrightarrow{BO}$=$\overrightarrow{BD}$-$\overrightarrow{OD}$=$\frac{1}{2}$$\overrightarrow{BC}$-$\frac{1}{3}$($\overrightarrow{AB}$+$\overrightarrow{AC}$)=$\frac{1}{2}$($\overrightarrow{AC}$-$\overrightarrow{AB}$)-$\frac{1}{3}$($\overrightarrow{AB}$+$\overrightarrow{AC}$)=-$\frac{5}{6}$$\overrightarrow{AB}$+$\frac{1}{6}$$\overrightarrow{AC}$.
故选:A.
点评 本题考查向量加法、减法及数乘的几何意义,向量的数乘运算,属于基础题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.在($\sqrt{3}$x+$\root{3}{2}$)100展开式所得的x的多项式中,系数为有理数的项有( )
| A. | 16项 | B. | 17项 | C. | 24项 | D. | 50项 |
17.某市每年中考都要举行实验操作考试和体能测试,初三(1)班共有30名学生,如图表格为该班学生的这两项成绩,表中实验操作考试和体能测试都为优秀的学生人数为6人.由于部分数据丢失,只知道从这班30人中随机抽取一个,实验操作成绩合格,且体能测试成绩合格或合格以上的概率是$\frac{1}{6}$.
(Ⅰ)试确定a,b的值;
(Ⅱ)从30人中任意抽取3人,设实验操作考试和体能测试成绩都是良好或优秀的学生人数为X,求随机变量X的分布列及数学期望E(X).
| 实验操作 | |||||
| 不合格 | 合格 | 良好 | 优秀 | ||
| 体能测试 | 不合格 | 0 | 1 | 1 | 1 |
| 合格 | 0 | 2 | 1 | b | |
| 良好 | 1 | a | 2 | 4 | |
| 优秀 | 1 | 1 | 3 | 6 | |
(Ⅱ)从30人中任意抽取3人,设实验操作考试和体能测试成绩都是良好或优秀的学生人数为X,求随机变量X的分布列及数学期望E(X).
11.设f(x)是定义在R上周期为2的奇函数,当0≤x≤1时,f(x)=x2-x,则$f({-\frac{5}{2}})$=( )
| A. | $-\frac{1}{4}$ | B. | $-\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
 设椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的长轴长为6,离心率$e=\frac{{\sqrt{6}}}{3}$,O为坐标原点.
设椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的长轴长为6,离心率$e=\frac{{\sqrt{6}}}{3}$,O为坐标原点.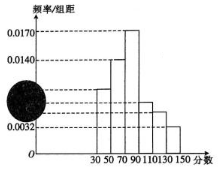 2017年省内事业单位面向社会公开招聘工作人员,为保证公平竞争,报名者需要参加笔试和面试两部分,且要求笔试成绩必须大于或等于90分的才有资格参加面试,90分以下(不含90分)则被淘汰.现有2000名竞聘者参加笔试,参加笔试的成绩按区间[30,50),[50,70),[70,90),[90,110),[110,130),[130,150]分段,其频率分布直方图如下图所示(频率分布直方图有污损),但是知道参加面试的人数为500,且笔试成绩在的人数为1440.
2017年省内事业单位面向社会公开招聘工作人员,为保证公平竞争,报名者需要参加笔试和面试两部分,且要求笔试成绩必须大于或等于90分的才有资格参加面试,90分以下(不含90分)则被淘汰.现有2000名竞聘者参加笔试,参加笔试的成绩按区间[30,50),[50,70),[70,90),[90,110),[110,130),[130,150]分段,其频率分布直方图如下图所示(频率分布直方图有污损),但是知道参加面试的人数为500,且笔试成绩在的人数为1440.