题目内容
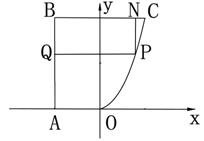
某地兴建一休闲商业广场，欲在如图所示的一块不规则用地规划建成一个矩形的商业楼区，余下作为休闲区域，已知
，且AB=BC=2AO=4km，曲线段OC是以O为顶点且开口向上的抛物线的一段，如果要使矩形的相邻两边分别落在AB、BC上，且一个顶点落在曲线段OC上，应如何规划才能使矩形商业楼区的用地面积最大？
如图，以O为原点，OA所在直线为x轴，建立直角坐标系，设抛物线方程为
代入点C（2，4）得
，
所以抛物线C方程为
设
，
，
S=
（6分）
由
，得
或
因为
，所以
当
时，
，S是x的增函数
当
时，
，S是x的减函数
所以，当
时，
取得最大值 （10分）
此时，
，
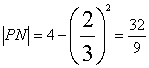
故把商业楼区规划成长为
，宽为
的矩形时，用地面积可最大
（13分）
练习册系列答案
相关题目
（2012•湖北模拟）某地兴建一休闲商业广场，欲在如图所示的一块不规则用地规划建成一个矩形的商业楼区，余下作为休闲区域，已知AB⊥BC，OA∥BC，且AB=BC=2AO=4km，曲线段OC是以O为顶点且开口向上的抛物线的一段，如果要使矩形的相邻两边分别落在AB、BC上，且一个顶点落在曲线段OC上，应如何规划才能使矩形商业楼区的用地面积最大？
，且AB=BC=2AO=4km，曲线段OC是以O为顶点且开口向上的抛物线的一段，如果要使矩形的相邻两边分别落在AB、BC上，且一个顶点落在曲线段OC上，应如何规划才能使矩形商业楼区的用地面积最大？
BC，且AB=BC=2AO=4km，曲线段OC是以O为顶点且开口向上的抛物线的一段，如果要使矩形的相邻两边分别落在AB、BC上，且一个顶点落在曲线段OC上，应如何规划才能使矩形商业楼区的用地面积最大？
