题目内容
11.已知幂函数y=f(x)的图象经过点(3,$\sqrt{3}$),那么f(4)=2.分析 利用待定系数法求出幂函数y=f(x)的解析式,再计算f(4)的值.
解答 解:设幂函数y=f(x)=xα,
其函数图象经过点(3,$\sqrt{3}$),
∴3α=$\sqrt{3}$,
解得α=$\frac{1}{2}$,
∴f(x)=${x}^{\frac{1}{2}}$=$\sqrt{x}$,
∴f(4)=2.
故答案为:2.
点评 本题考查了用待定系数法求出幂函数的解析式以及函数求值的应用问题,是基础题目.

练习册系列答案
相关题目
19.已知f(x)=x2+2x,则f′(2)=( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
16.过点(0,-2)与抛物线y2=8x只有一个公共点的直线有( )
| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
1.设双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的右焦点是F,左、右顶点分别是A1,A2,过F做直线A1A2的垂线与双曲线交于B,C两点,若A1B⊥A2C,则该双曲线的离心率为( )
| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{3}{2}$ | D. | $\sqrt{2}$ |
 已知函数f(x)=cos(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象,如图所示.
已知函数f(x)=cos(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象,如图所示.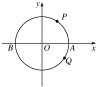 如图,动点P,Q从点A(3,0)出发绕⊙O作圆周运动,若点M按逆时针方向每秒钟转$\frac{π}{3}$rad,点N按顺时针方向每秒钟转$\frac{π}{6}$rad.则当M、N第一次相遇时,点M转过的弧长为4π.
如图,动点P,Q从点A(3,0)出发绕⊙O作圆周运动,若点M按逆时针方向每秒钟转$\frac{π}{3}$rad,点N按顺时针方向每秒钟转$\frac{π}{6}$rad.则当M、N第一次相遇时,点M转过的弧长为4π. 已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上顶点A(0,2),右焦点F(1,0),设椭圆上任一点到点M(0,6)的距离为d.
已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上顶点A(0,2),右焦点F(1,0),设椭圆上任一点到点M(0,6)的距离为d.