题目内容
如果圆锥底面半径为r,轴截面为等腰直角三角形,那么圆锥的侧面积为( )
分析:根据圆锥的底面半径及轴截面为等腰直角三角形,然后求出圆锥的母线,即可求解圆锥的侧面积.
解答:解:∵圆锥的轴截面是等腰直角三角形,圆锥的底面半径为r,
圆锥的轴截面是等腰直角三角形,
∴圆锥的母线长为
r,
底面周长为:2πr.
圆锥的侧面积为:
×2πr×
r=
πr2.
故选A.
圆锥的轴截面是等腰直角三角形,
∴圆锥的母线长为
| 2 |
底面周长为:2πr.
圆锥的侧面积为:
| 1 |
| 2 |
| 2 |
| 2 |
故选A.
点评:本题考查圆锥的计算,得到圆锥的底面半径是解决本题的突破点;注意圆锥的侧面积=
×底面周长×母线长的应用.
| 1 |
| 2 |

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目

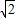 πr2
πr2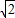 +1)πr2
+1)πr2 (
(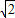 +1)πr2
+1)πr2 πr2
πr2