题目内容
方程（
）|x|-m=0有解，则m的取值范围为
- A.0＜m≤1
- B.m≥1
- C.m≤-1
- D.0≤m＜1
A
分析：首先对等式移项，把求方程
有解，m的取值范围转化为求函数值域问题，求
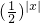的值域问题，首先考虑|x|是大于0的，在这个条件下根据指数函数的值域的求法，求得m的取值范围．
解答：由（）|x|-m=0得，m=（）|x|，
∵|x|≥0，∴0＜（）|x|≤1，
∴方程（）|x|-m=0有解，必须0＜m≤1，
故答案选A．
点评：此题主要考查的是函数和方程的综合应用问题，把求m的取值范围转化为求函数值域问题，这个思想在求取值范围的时候应用广泛，值得注意．
分析：首先对等式移项，把求方程
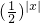有解，m的取值范围转化为求函数值域问题，求的值域问题，首先考虑|x|是大于0的，在这个条件下根据指数函数的值域的求法，求得m的取值范围．解答：由（
）|x|-m=0得，m=（）|x|，∵|x|≥0，∴0＜（
）|x|≤1，∴方程（
）|x|-m=0有解，必须0＜m≤1，故答案选A．
点评：此题主要考查的是函数和方程的综合应用问题，把求m的取值范围转化为求函数值域问题，这个思想在求取值范围的时候应用广泛，值得注意．
练习册系列答案
状元坊全程突破导练测系列答案
相关题目