题目内容
已知椭圆E: +y2=1(a>1)的上顶点为M(0,1),两条过M的动弦MA、MB满足MA⊥MB.
+y2=1(a>1)的上顶点为M(0,1),两条过M的动弦MA、MB满足MA⊥MB.
(1)当坐标原点到椭圆E的准线距离最短时,求椭圆E的方程;
(2)若Rt△MAB面积的最大值为 ,求a;
,求a;
(3)对于给定的实数a(a>1),动直线AB是否经过一定点?如果经过,求出定点坐标(用a表示);反之,说明理由.
 +y2=1(a>1)的上顶点为M(0,1),两条过M的动弦MA、MB满足MA⊥MB.
+y2=1(a>1)的上顶点为M(0,1),两条过M的动弦MA、MB满足MA⊥MB.(1)当坐标原点到椭圆E的准线距离最短时,求椭圆E的方程;
(2)若Rt△MAB面积的最大值为
 ,求a;
,求a;(3)对于给定的实数a(a>1),动直线AB是否经过一定点?如果经过,求出定点坐标(用a表示);反之,说明理由.
(1) +y2=1.(2)a=3(3)
+y2=1.(2)a=3(3)
 +y2=1.(2)a=3(3)
+y2=1.(2)a=3(3)
(1)由题,a2=c2+1,d= =
= =c+
=c+ ≥2,当c=1时取等号,此时a2=1+1=2,故椭圆E的方程为
≥2,当c=1时取等号,此时a2=1+1=2,故椭圆E的方程为 +y2=1.
+y2=1.
(2)不妨设直线MA的斜率k>0,直线MA方程为y=kx+1,由
①代入②整理得(a2k2+1)x2+2a2kx=0,
解得xA=- ,故A
,故A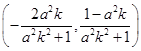 ,
,
由MA⊥MB知直线MB的斜率为- ,可得B
,可得B ,
,
则MA= ,MB=
,MB= .
.
则S△MAB= MA·MB=
MA·MB= (1+k2)
(1+k2)
= .
.
令k+ =t(t≥2),
=t(t≥2),
则S△MAB= .
.
当t= 时取“=”,∵t=
时取“=”,∵t= ≥2,得a>
≥2,得a> +1.而(S△MAB)max=
+1.而(S△MAB)max= ,故a=3或a=
,故a=3或a= (舍).综上a=3.
(舍).综上a=3.
(3)由对称性,若存在定点,则必在y轴上.
当k=1时,A ,直线AB过定点Q
,直线AB过定点Q .下面证明A、Q、B三点共线:
.下面证明A、Q、B三点共线:
∵kAQ= ,
,
kBQ= .
.
由kAQ=kBQ知A、Q、B三点共线,即直线AB过定点Q .
.
 =
= =c+
=c+ ≥2,当c=1时取等号,此时a2=1+1=2,故椭圆E的方程为
≥2,当c=1时取等号,此时a2=1+1=2,故椭圆E的方程为 +y2=1.
+y2=1.(2)不妨设直线MA的斜率k>0,直线MA方程为y=kx+1,由

①代入②整理得(a2k2+1)x2+2a2kx=0,
解得xA=-
 ,故A
,故A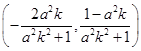 ,
,由MA⊥MB知直线MB的斜率为-
 ,可得B
,可得B ,
,则MA=
 ,MB=
,MB= .
.则S△MAB=
 MA·MB=
MA·MB= (1+k2)
(1+k2)
=
 .
.令k+
 =t(t≥2),
=t(t≥2),则S△MAB=
 .
.当t=
 时取“=”,∵t=
时取“=”,∵t= ≥2,得a>
≥2,得a> +1.而(S△MAB)max=
+1.而(S△MAB)max= ,故a=3或a=
,故a=3或a= (舍).综上a=3.
(舍).综上a=3.(3)由对称性,若存在定点,则必在y轴上.
当k=1时,A
 ,直线AB过定点Q
,直线AB过定点Q .下面证明A、Q、B三点共线:
.下面证明A、Q、B三点共线:∵kAQ=
 ,
,kBQ=
 .
.由kAQ=kBQ知A、Q、B三点共线,即直线AB过定点Q
 .
.
练习册系列答案
相关题目
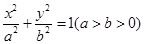 的离心率是
的离心率是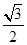 .
.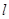 ,使点C(2,0)关于直线
,使点C(2,0)关于直线 中,点P到两圆C1与C2的圆心的距离之和等于4,其中C1:
中,点P到两圆C1与C2的圆心的距离之和等于4,其中C1: ,C2:
,C2: . 设点P的轨迹为
. 设点P的轨迹为 .
. 与C交于A,B两点.问k为何值时
与C交于A,B两点.问k为何值时

 ?此时
?此时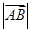 的值是多少?
的值是多少?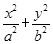 =1(a>b>0,a、b为常数),动圆C1:x2+y2=
=1(a>b>0,a、b为常数),动圆C1:x2+y2=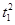 ,b<t1<a.点A1、A2分别为C0的左、右顶点,C1与C0相交于A、B、C、D四点.
,b<t1<a.点A1、A2分别为C0的左、右顶点,C1与C0相交于A、B、C、D四点.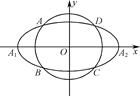
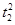 与C0相交于A′,B′,C′,D′四点,其中b<t2<a,t1≠t2.若矩形ABCD与矩形A′B′C′D′的面积相等,证明:
与C0相交于A′,B′,C′,D′四点,其中b<t2<a,t1≠t2.若矩形ABCD与矩形A′B′C′D′的面积相等,证明: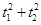 为定值.
为定值. =1(a>b>0)的焦点为F1与F2,且P∈E,∠F1PF2=2θ.求证:△PF1F2的面积S=b2tanθ.
=1(a>b>0)的焦点为F1与F2,且P∈E,∠F1PF2=2θ.求证:△PF1F2的面积S=b2tanθ.
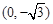 )和
)和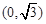 ,并且经过点
,并且经过点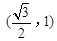 ,抛物线的顶点E在坐标原点,焦点恰好是椭圆C的右顶点F.
,抛物线的顶点E在坐标原点,焦点恰好是椭圆C的右顶点F.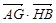 的最小值.
的最小值.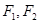 是椭圆的两个焦点,过
是椭圆的两个焦点,过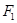 且与椭圆长轴垂直的直线交椭圆于A、B两点,若
且与椭圆长轴垂直的直线交椭圆于A、B两点,若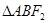 是正三角形,则这个椭圆的离心率是( )
是正三角形,则这个椭圆的离心率是( )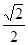 B.
B.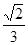 C.
C.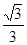 D.
D.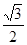
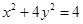 上的一点,P点是椭圆上的动点,
上的一点,P点是椭圆上的动点,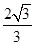
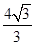
 +y2=1上,顶点A与椭圆的焦点F1重合,且椭圆的另外一个焦点F2在BC边上,则△ABC的周长是________.
+y2=1上,顶点A与椭圆的焦点F1重合,且椭圆的另外一个焦点F2在BC边上,则△ABC的周长是________.