题目内容
已知![]() 为坐标原点,点
为坐标原点,点![]() 、
、![]() 的坐标分别为(
的坐标分别为(![]() ,0)、(
,0)、(![]() ,0),点
,0),点![]() 、
、![]() 满足
满足![]() ,
,![]() ,过点
,过点![]() 且垂直于
且垂直于![]() 的直线交线段
的直线交线段![]() 于点
于点![]() ,设点
,设点![]() 的轨迹为
的轨迹为![]() .
.
(1)求轨迹![]() 的方程;
的方程;
(2)若轨迹![]() 上存在两点
上存在两点![]() 和
和![]() 关于直线
关于直线![]() :
:![]() (
(![]() )对称,求
)对称,求![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,设直线![]() 与轨迹
与轨迹![]() 交于不同的两点
交于不同的两点![]() 、
、![]() ,对点
,对点![]() (1,0)和向量
(1,0)和向量![]() (
(![]() ,3
,3![]() ),求
),求![]() 取最大值时直线
取最大值时直线![]() 的方程.
的方程.
解:(Ⅰ)∵![]() ,∴
,∴![]() 为
为![]() 中点.
中点.
∴![]() 垂直平分
垂直平分![]() .
.
∴![]() .
.
∴![]() .
.
∴点![]() 的轨迹
的轨迹![]() 是以正
是以正![]() 、
、![]() 为焦点的椭圆.
为焦点的椭圆.
∴长半轴![]() ,半焦距
,半焦距![]() ,
,
∴![]() .
.
∴点![]() 的轨迹方程为
的轨迹方程为![]()
(2)设![]() ,
,![]() ,
,![]() 的中点
的中点![]() .
.
由
![]() .
.
又![]() ,∴
,∴![]() ,
,![]() .
.
∵中点![]() 在椭圆内部,∴
在椭圆内部,∴![]()
∴![]() (-1,0)∪(0,1).
(-1,0)∪(0,1).
(3)将![]()
![]() 代入椭圆
代入椭圆![]() 中,整理得
中,整理得
![]() .
.
设![]() (
(![]() ,
,![]() ),
),![]() (
(![]() ,
,![]() ).
).
则![]() +
+![]() =
=![]() ,
,![]()
![]() =
=![]() .
.
∴![]()
![]() =
=![]() =
=![]() =
=![]()
∴![]()
=![]()
![]()
=![]()

![]() .
.
当仅当 ,即
,即![]() (0,1)时等号成立.
(0,1)时等号成立.
此时,直线![]() (
(![]() +1).
+1).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
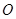 为坐标原点,点
为坐标原点,点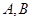 分别在
分别在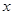 轴
轴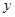 轴上运动,且
轴上运动,且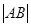 =8,动点
=8,动点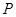 满足
满足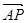 =
=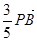 ,设点
,设点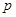 的轨迹为曲线
的轨迹为曲线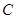 ,定点为
,定点为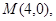 直线
直线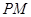 交曲线
交曲线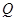
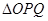 面积的最大值。
面积的最大值。 为坐标原点,点
为坐标原点,点 ,点
,点 满足条件
满足条件 ,则
,则 的最大值为_____________。
的最大值为_____________。 ,
, ,
, 为坐标原点,点
为坐标原点,点 在第四象限内,且
在第四象限内,且 ,设
,设
 ,则
,则 的值是( )
的值是( ) .
.
 .
.

 .
.
 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为 ,点
,点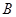 的坐标为
的坐标为 ,其中
,其中 且
且 .设
.设 .
. ,
, ,
, ,求方程
,求方程 在区间
在区间 内的解集;
内的解集; 上的动点.当
上的动点.当 时,设函数
时,设函数 的值域为集合
的值域为集合 ,不等式
,不等式 的解集为集合
的解集为集合 . 若
. 若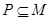 恒成立,求实数
恒成立,求实数 的最大值;
的最大值; 、
、 和
和 的值. 当
的值. 当 对称,且在
对称,且在 处
处 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 ,其中
,其中 且
且 .设
.设 .
. ,
, ,
, ,求方程
,求方程 在区间
在区间 内的解集;
内的解集; 且法向量为
且法向量为 的直线
的直线 上的动点.当
上的动点.当 时,设函数
时,设函数 的值域为集合
的值域为集合 ,不等式
,不等式 的解集为集合
的解集为集合 . 若
. 若 恒成立,求实数
恒成立,求实数 的最大值;
的最大值; 、
、 和
和 的值. 当
的值. 当 对称,且在
对称,且在 处
处