题目内容
(本小题满分12分)
已知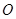 为坐标原点,点
为坐标原点,点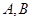 分别在
分别在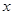 轴
轴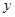 轴上运动,且
轴上运动,且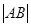 =8,动点
=8,动点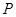 满足
满足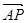 =
=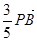 ,设点
,设点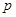 的轨迹为曲线
的轨迹为曲线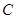 ,定点为
,定点为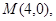 直线
直线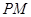 交曲线
交曲线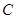 于另外一点
于另外一点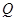
(1)求曲线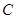 的方程;
的方程;
(2)求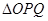 面积的最大值。
面积的最大值。
【答案】
(1)  (2)
(2) 
【解析】
试题分析:解:(1)设 则
则 ,
,

又
 曲线C的方程为
曲线C的方程为
(2)由(1)可知,M(4,0)为椭圆 的右焦点,设直线PM方程为
的右焦点,设直线PM方程为 ,代入
,代入 ,得
,得


 =
= =
= =
=

当 ,即
,即 时,
时, 的面积取得最大值
的面积取得最大值
此时直线方程为
考点:本试题考查了直线方程与椭圆的知识。
点评:解决该试题的关键是能利用已知中的点和斜率来借助于点斜式方程表示出直线的方程,同时能结合直线与椭圆的相交,联立方程组,进而结合韦达定理和判别式来求解表示出长轴长,借助于参数a的范围得到所求的最值,属于中档题。

练习册系列答案
相关题目