设随机变量x-N=P.则P=1-2p．题目和参考答案——青夏教育精英家教网—

题目内容

18．设随机变量x～N（3，1），若P（X＞4）=P，则P（2＜X＜4）=1-2p．

分析根据题目中：“正态分布N（3，1）”，画出其正态密度曲线图：根据对称性，由P（X＞4）=p的概率可求出P（2＜X＜4）．

解答解：∵随机变量X～N（3，1），观察图得，
P（2＜X＜4）=1-2P（X＞4）=1-2p．
故答案为：1-2p．

点评本题主要考查正态分布曲线的特点及曲线所表示的意义，注意根据正态曲线的对称性解决问题．

练习册系列答案

9．某校田径队共有男运动员45人，女运动员36人．若采用分层抽样的方法在全体运动员中抽取18人进行体质测试，则抽到的女运动员人数为8．

6．设a=lg5，b=log₂$\sqrt{2}$，c=ln3，则（　　）

13．如图所示的程序框图，输出的结果S的值为（　　）

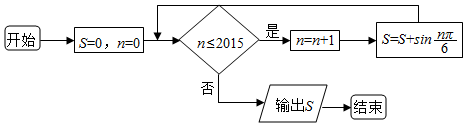
$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$

D．

$\frac{3}{2}$+$\frac{\sqrt{3}}{2}$

3．

如图，已知四边形ABCD是梯形，E，F分别是腰的中点，M，N是线段EF上的两个点，且EM=MN=NF，下底是上底的2倍，若$\overrightarrow{AB}=\overrightarrow a，\overrightarrow{BC}=\overrightarrow b$，则$\overrightarrow{DN}$=（　　）

A．

$-\frac{1}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b$

B．

$\frac{1}{4}\overrightarrow a+\frac{1}{2}\overrightarrow b$

C．

$\frac{1}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b$

D．

$\frac{1}{4}\overrightarrow a-\frac{1}{2}\overrightarrow b$

10．若随机变量ξ的分布列为P（ξ=k）=ak（k=1，2，3），则实数a=$\frac{1}{6}$；数学期望Eξ=$\frac{7}{3}$．

2．双曲线C：$\frac{{x}^{2}}{8}$-$\frac{{y}^{2}}{8}$=1，又A∈C，已知A（4，2$\sqrt{2}$），F（4，0），若由F射至A的光线被双曲线C反射，反射光线通过P（8，k），则k=$3\sqrt{2}$．

3．下列命题中错误的是（　　）

	A．	命题“?x∈[0，1]，使x²-1≥0的否定为“?x∈[0，1]，都有x²-1＜0”
	B．	命题p为假命题，命题q为真命题，则（￢p）∨（￢q）为真命题
	C．	命题“若x，y均为奇数，则x+y为奇数”及它的逆命题均为假命题
	D．	命題“若x²+2x=0，则x=0或x=2”的逆否命题为“若x≠0或x≠2，则x²+2x≠0”．

试题分类