题目内容
(本小题满分12分)
甲乙两名射手互不影响地进行射击训练,根据以往的数据统计,他们设计成绩的分布列如下:
(Ⅰ)若甲乙两射手各射击两次,求四次射击中恰有三次命中10环的概率;
(Ⅱ)若两个射手各射击1次,记所得的环数之和为 ,求
,求 的分布列和期望.
的分布列和期望.
甲乙两名射手互不影响地进行射击训练,根据以往的数据统计,他们设计成绩的分布列如下:
| 射手甲 | 射手乙 | ||||||
| 环数 | 8 | 9 | 10 | 环数 | 8 | 9 | 10 |
| 概率 |  |  |  | 概率 |  |  |  |
(Ⅱ)若两个射手各射击1次,记所得的环数之和为
 ,求
,求 的分布列和期望.
的分布列和期望. (Ⅰ) ;(Ⅱ)
;(Ⅱ)
 ;(Ⅱ)
;(Ⅱ)
(1)若甲乙两射手各射击两次,四次射击中恰有三次命中10环分两类:甲命中1次10环,乙命中两次10环和甲命中2次10环,乙命中1次10环,分别求概率再求和;
(2)ξ的取值分别为16,17,18,19,20,利用独立事件的概率求法分别求ξ取每个值的概率即可.再列出分布列,求出期望.
解;(Ⅰ)记事件 甲命中1次10环,乙命中两次10环,事件
甲命中1次10环,乙命中两次10环,事件 ;甲命中2次10环,乙命中1次10环,则四次射击中恰有三次命中10环为事件
;甲命中2次10环,乙命中1次10环,则四次射击中恰有三次命中10环为事件

 (6 分)
(6 分)
(Ⅱ) 的取值分别为16,17,18,19,20,
的取值分别为16,17,18,19,20,  (9 分)
(9 分)

 (12分)
(12分)
(2)ξ的取值分别为16,17,18,19,20,利用独立事件的概率求法分别求ξ取每个值的概率即可.再列出分布列,求出期望.
解;(Ⅰ)记事件
 甲命中1次10环,乙命中两次10环,事件
甲命中1次10环,乙命中两次10环,事件 ;甲命中2次10环,乙命中1次10环,则四次射击中恰有三次命中10环为事件
;甲命中2次10环,乙命中1次10环,则四次射击中恰有三次命中10环为事件

 (6 分)
(6 分)(Ⅱ)
 的取值分别为16,17,18,19,20,
的取值分别为16,17,18,19,20,  (9 分)
(9 分)
 (12分)
(12分)
练习册系列答案
相关题目

 表示抽到“极幸福”的人数,求
表示抽到“极幸福”的人数,求 .
. 为在体操岗位服务的美国志愿者的个数,求
为在体操岗位服务的美国志愿者的个数,求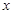 个红球与
个红球与 个白球(
个白球( ,且
,且 ),乙箱中放有2个红球、1个白球与1个黑球。从甲箱中任取2个球,从乙箱中任取1个球。
),乙箱中放有2个红球、1个白球与1个黑球。从甲箱中任取2个球,从乙箱中任取1个球。 ,求当
,求当 时,求取出的3个球中红球个数
时,求取出的3个球中红球个数 的期望
的期望 。
。 。
。 层楼,写出
层楼,写出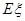 。
。 的所有非空子集中,等可能地取出一个.
的所有非空子集中,等可能地取出一个.  :集合中的所有元素之和为10,求所取出的非空子集满足性质
:集合中的所有元素之和为10,求所取出的非空子集满足性质 ,求
,求 .
. 、
、 、
、 ;已知乙项目的利润与产品价格的调整有关,在每次调整中价格下降的概率都是
;已知乙项目的利润与产品价格的调整有关,在每次调整中价格下降的概率都是 ,设乙项目产品价格在一年内进行2次独立的调整,记乙项目产品价格在一年内的下降次数为
,设乙项目产品价格在一年内进行2次独立的调整,记乙项目产品价格在一年内的下降次数为 ,对乙项目投资十万元,
,对乙项目投资十万元,  、
、 分别表示对甲、乙两项目各投资十万元一年后的利润.
分别表示对甲、乙两项目各投资十万元一年后的利润. 、
、 ;
; 时,求
时,求 的取值范围.
的取值范围.  表示4名乘客在第4层下电梯的人数,则
表示4名乘客在第4层下电梯的人数,则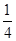 ,8∶20发出的概率为
,8∶20发出的概率为 ,8∶40发出的概率为
,8∶40发出的概率为 的分布列和数学期望。
的分布列和数学期望。