题目内容

如图已知直三棱柱ABC—A1B1C1中，∠ACB=90°，∠BAC=30°，BC=1，AA1=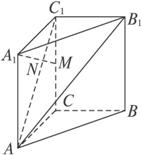，M为CC1的中点，求证：AB1⊥A1M.

证明:∵B1C1⊥C1C，B1C1⊥A1C1，

∴B1C1⊥面ACC1A1.

∴AC1是AB1在平面ACC1A1上的射影.

连结AC1交A1M于N，在△ABC中，

∠BAC=30°，∠ACB=90°，

∴AC=.

∵，

∴△ACC1∽△MC1A1.

于是A1M⊥AC1.

∴由三垂线定理知AB1⊥A1M.

练习册系列答案
相关题目
精英家教网如图，已知直三棱柱ABC-A1B1C1，侧棱长为2，底面△ABC中，∠B=90°，AB=1，BC=
3
，D是侧棱CC1上一点，且BD与底面所成角为30°．
（1）求点D到AB所在直线的距离．
（2）求二面角A1-BD-B1的度数．
如图，已知直三棱柱ABC-A1B1C1中，AC=BC=2，M，N分别是棱CC1，AB的中点．
（Ⅰ）求证：平面MCN⊥平面ABB1A1；
（Ⅱ）求证：CN∥平面AMB1．
（2007•温州一模）已知直三棱柱ABC-A1B1C1（如图），若AB=BC=3，AA1=6，且AB⊥BC．
（Ⅰ）求点B到平面AA1C1C的距离；
（Ⅱ）设D为BB1中点，求平面A1CD与底面A1B1C1所成二面角的余弦值．
如图,已知直三棱柱ABC—A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,D是AA1的中点.

(1)求异面直线AB和C1D所成的角;

(2)设E是AB上一点,试确定E点的位置,使得A1E⊥C1D;

(3)在(2)的条件下,求点D到平面B1C1E的距离.

如图,已知直三棱柱ABC—A1B1C1的侧棱AA1=4 cm,它的底面ABC中有AC=BC=2 cm,∠ACB=90°,E是AB的中点.

(1)求证:CE⊥AB1;

(2)求C到AB1的距离;

(3)求二面角C—AB1—B的余弦值.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网