题目内容
(1)A(-2,0)、B(2,0),M满足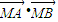 =0,求M轨迹.
=0,求M轨迹.(2)若(1)中的轨迹按向量(1,-1)平移后恰与x+ky-3=0相切,求k.
(3)如图,l过
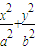 =1 (a>b>0)长轴顶点A且与长轴垂直的直线,E、F是两焦点,P∈l,P、A不重合,若∠EPF=α,则有0<α≤arctan
=1 (a>b>0)长轴顶点A且与长轴垂直的直线,E、F是两焦点,P∈l,P、A不重合,若∠EPF=α,则有0<α≤arctan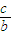 ,类比此结论到
,类比此结论到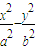 =1 (a>0,b>0),l是过焦点F且垂直x轴的直线,A、B是两顶点,P∈l,P、F不重合,∠APB=α,求α取值范围.
=1 (a>0,b>0),l是过焦点F且垂直x轴的直线,A、B是两顶点,P∈l,P、F不重合,∠APB=α,求α取值范围.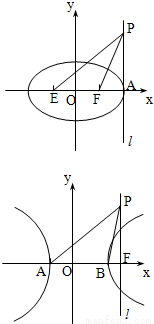
【答案】分析:(1)设点M为(x,y)代入题目中的条件 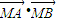 =0可得x2+y2=4即得到点M的轨迹方程.
=0可得x2+y2=4即得到点M的轨迹方程.
(2)由题意得得到新的圆的方程(x-1)2+(y+1)2=4,由其与直线x+ky-3=0 相切可得k=0或 .
.
(3)类比椭圆的证明方法得到双曲线的类似的性质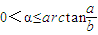 .
.
解答:解:(1)设 ,
,
所以点M的轨迹方程为x2+y2=4.
(2)将x2+y2=4向右平移一个单位,再向下平移一个单位后,得到圆(x-1)2+(y+1)2=4,
因为圆平移后恰与x+ky-3=0相切,
所以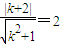 ,
,
得k=0或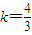 .
.
(3)由题意可得:不妨设P(c,t)(t>0),
则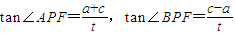
所以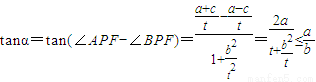
所以0<tanα≤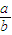 .显然α为锐角,即:0<α≤arctan
.显然α为锐角,即:0<α≤arctan 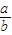
所以α取值范围为: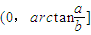 .
.
点评:解决此类问题的关键是熟练的把向量条件坐标化以及类比推理的有关知识,熟练掌握直线与圆的位置关系以及椭圆与双曲线的几何性质,考查运算能力和综合解题能力.
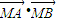 =0可得x2+y2=4即得到点M的轨迹方程.
=0可得x2+y2=4即得到点M的轨迹方程.(2)由题意得得到新的圆的方程(x-1)2+(y+1)2=4,由其与直线x+ky-3=0 相切可得k=0或
 .
.(3)类比椭圆的证明方法得到双曲线的类似的性质
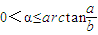 .
.解答:解:(1)设
 ,
,所以点M的轨迹方程为x2+y2=4.
(2)将x2+y2=4向右平移一个单位,再向下平移一个单位后,得到圆(x-1)2+(y+1)2=4,
因为圆平移后恰与x+ky-3=0相切,
所以
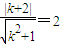 ,
,得k=0或
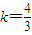 .
.(3)由题意可得:不妨设P(c,t)(t>0),
则
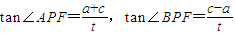
所以
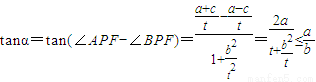
所以0<tanα≤
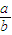 .显然α为锐角,即:0<α≤arctan
.显然α为锐角,即:0<α≤arctan 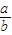
所以α取值范围为:
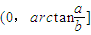 .
.点评:解决此类问题的关键是熟练的把向量条件坐标化以及类比推理的有关知识,熟练掌握直线与圆的位置关系以及椭圆与双曲线的几何性质,考查运算能力和综合解题能力.

练习册系列答案
相关题目
 (1)A(-2,0)、B(2,0),M满足
(1)A(-2,0)、B(2,0),M满足