题目内容
已知抛物线Γ:y2=2px(p>0)的焦点与椭圆4x2+20y2=5的右焦点重合.
(Ⅰ)求抛物线Γ的方程;
(Ⅱ)动直线l恒过点M(0,1)与抛物线Γ交于A、B两点,与x轴交于C点,请你观察并判断:在线段MA,MB,MC,AB中,哪三条线段的长总能构成等比数列?说明你的结论并给出证明.
解:(Ⅰ)∵椭圆方程为: ,∴
,∴ ,…(2分)
,…(2分)
∴c2=1,即椭圆的右焦点为(1,0),
因为抛物线的焦点为( ,0),所以p=2,…(3分)
,0),所以p=2,…(3分)
所以抛物线的方程为y2=4x.…(4分)
(Ⅱ)解法一:设直线l:y=kx+1(k≠0),则C(- ,0),
,0),
由 得k2x2+2(k-2)x+1=0,…(6分)
得k2x2+2(k-2)x+1=0,…(6分)
因为△=4(k-2)2-4k2>0,所以k<1,…(7分)
设A(x1,y1),B(x2,y2),则 ,
, ,…(8分)
,…(8分)
所以由弦长公式得: ,
, ,
, ,
, ,…(10分)
,…(10分)
|MA|•|MB|=(1+k2)•|x1x2|=(1+k2)•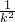 =|MC|2.…(11分)
=|MC|2.…(11分)
若|MA|•|MB|=|AB|2,则 ,不满足题目要求.…(12分)
,不满足题目要求.…(12分)
所以存在三线段MA、MC、MB的长成等比数列.…(13分)
解法二:同法一得 ,…(8分)
,…(8分)
而 =(x1,y1-1)•(x2,y2-1)=(x1,kx1)•(x2,kx2)
=(x1,y1-1)•(x2,y2-1)=(x1,kx1)•(x2,kx2)
=(1+k2)x1x2= =
= ,
,
因为C(- ,0),所以|MC|2=1+
,0),所以|MC|2=1+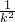 .…(10分)
.…(10分)
因为M、A、B三点共线,且向量 、
、 同向,
同向,
所以 =
= =
= ,…(11分)
,…(11分)
因此 =
= =|MC|2.
=|MC|2.
所以存在三线段MA、MC、MB的长成等比数列.…(13分)
分析:(Ⅰ)化椭圆方程为标准方程,确定椭圆的右焦点,可得抛物线的焦点,进而可得抛物线的方程;
(Ⅱ)解法一:设直线l的方程代入到抛物线方程,利用韦达定理及弦长公式,确定线段MA,MB,MC,AB的长,计算可得结论;
解法二:利用向量的方法,确定M、A、B三点共线,且 =
= =|MC|2.
=|MC|2.
点评:本题考查椭圆的方程与性质,考查抛物线的方程,考查直线与武平县的位置关系,考查韦达定理的运用,考查等比数列的判定,属于中档题.
 ,∴
,∴ ,…(2分)
,…(2分)∴c2=1,即椭圆的右焦点为(1,0),
因为抛物线的焦点为(
 ,0),所以p=2,…(3分)
,0),所以p=2,…(3分)所以抛物线的方程为y2=4x.…(4分)
(Ⅱ)解法一:设直线l:y=kx+1(k≠0),则C(-
 ,0),
,0),由
 得k2x2+2(k-2)x+1=0,…(6分)
得k2x2+2(k-2)x+1=0,…(6分)因为△=4(k-2)2-4k2>0,所以k<1,…(7分)
设A(x1,y1),B(x2,y2),则
 ,
, ,…(8分)
,…(8分)所以由弦长公式得:
 ,
, ,
, ,
, ,…(10分)
,…(10分)|MA|•|MB|=(1+k2)•|x1x2|=(1+k2)•
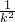 =|MC|2.…(11分)
=|MC|2.…(11分)若|MA|•|MB|=|AB|2,则
 ,不满足题目要求.…(12分)
,不满足题目要求.…(12分)所以存在三线段MA、MC、MB的长成等比数列.…(13分)
解法二:同法一得
 ,…(8分)
,…(8分)而
 =(x1,y1-1)•(x2,y2-1)=(x1,kx1)•(x2,kx2)
=(x1,y1-1)•(x2,y2-1)=(x1,kx1)•(x2,kx2)=(1+k2)x1x2=
 =
= ,
,因为C(-
 ,0),所以|MC|2=1+
,0),所以|MC|2=1+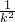 .…(10分)
.…(10分)因为M、A、B三点共线,且向量
 、
、 同向,
同向,所以
 =
= =
= ,…(11分)
,…(11分)因此
 =
= =|MC|2.
=|MC|2.所以存在三线段MA、MC、MB的长成等比数列.…(13分)
分析:(Ⅰ)化椭圆方程为标准方程,确定椭圆的右焦点,可得抛物线的焦点,进而可得抛物线的方程;
(Ⅱ)解法一:设直线l的方程代入到抛物线方程,利用韦达定理及弦长公式,确定线段MA,MB,MC,AB的长,计算可得结论;
解法二:利用向量的方法,确定M、A、B三点共线,且
 =
= =|MC|2.
=|MC|2.点评:本题考查椭圆的方程与性质,考查抛物线的方程,考查直线与武平县的位置关系,考查韦达定理的运用,考查等比数列的判定,属于中档题.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目