题目内容
13.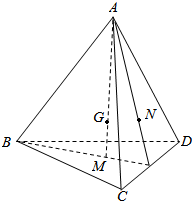 如图,已知M、N分别为四面体ABCD的面BCD与面ACD的重心,且G为AM上一点,且GM:GA=1:3,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,$\overrightarrow{AD}$=$\overrightarrow{c}$,试用$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$表示$\overrightarrow{BG}$,$\overrightarrow{BN}$.
如图,已知M、N分别为四面体ABCD的面BCD与面ACD的重心,且G为AM上一点,且GM:GA=1:3,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,$\overrightarrow{AD}$=$\overrightarrow{c}$,试用$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$表示$\overrightarrow{BG}$,$\overrightarrow{BN}$.
分析 根据向量的加减法计算即可.
解答 解:$\overrightarrow{BG}=\overrightarrow{BM}+\overrightarrow{MG}$
=$\overrightarrow{BM}-\frac{1}{4}\overrightarrow{AM}$
=$\overrightarrow{BM}-\frac{1}{4}(\overrightarrow{AB}+\overrightarrow{BM})$
=$\frac{3}{4}\overrightarrow{BM}-\frac{1}{4}\overrightarrow{a}$
=$\frac{3}{4}×\frac{2}{3}×\frac{1}{2}(\overrightarrow{BC}+\overrightarrow{BD})$-$\frac{1}{2}\overrightarrow{\overrightarrow{a}}$
=$\frac{1}{4}$($\overrightarrow{b}-\overrightarrow{a}+\overrightarrow{c}-\overrightarrow{a}$)-$\frac{1}{2}\overrightarrow{a}$
=-$\overrightarrow{a}+\frac{1}{4}\overrightarrow{b}+\frac{1}{4}\overrightarrow{c}$;
$\overrightarrow{BN}$=$\overrightarrow{AN}-\overrightarrow{AB}$
=$\frac{2}{3}×\frac{1}{2}(\overrightarrow{AC}+\overrightarrow{AD})-\overrightarrow{AB}$
=$\frac{1}{3}\overrightarrow{b}+\frac{1}{3}\overrightarrow{c}-\overrightarrow{a}$.
点评 本题主要考查向量的加减法和几何表示,属于基础题

| A. | f(x)=1,g(x)=x0 | B. | y=x与y=$\sqrt{{x}^{2}}$ | C. | y=x2与y=(x+1)2 | D. | f(x)=|x|,g(x)=$\sqrt{{x}^{2}}$ |
| A. | (-3,3) | B. | (-3,0)∪(3,+∞) | C. | (-∞,-3)∪(0,3) | D. | (-∞,-3)∪(3,+∞) |
| A. | (1,2) | B. | (2,3) | C. | (3,4) | D. | (4,5) |
| A. | 12 | B. | 8 | C. | 6 | D. | 4 |