题目内容
若直线
，（t为参数）与圆
，（θ为参数）相切，则b=
- A.-4或6
- B.-6或4
- C.-1或9
- D.-9或1
A
分析：先把参数方程化为普通方程，再利用直线与圆相切的充要条件是圆心到直线的距离等于半径，即可求出答案．
解答：把直线，（t为参数）与圆，（θ为参数）的参数方程分别化为普通方程得：
直线：4x+3y-3=0，圆：x2+（y-b）2=9，
∵此直线与该圆相切，∴
，解得b=-4，或6．
故选A．
点评：本题考查参数方程与普通方程的互化及直线与圆相切，充分利用直线与圆相切的充要条件是圆心到直线的距离等于半径是解决问题的关键．
分析：先把参数方程化为普通方程，再利用直线与圆相切的充要条件是圆心到直线的距离等于半径，即可求出答案．
解答：把直线
，（t为参数）与圆，（θ为参数）的参数方程分别化为普通方程得：直线：4x+3y-3=0，圆：x2+（y-b）2=9，
∵此直线与该圆相切，∴
，解得b=-4，或6．故选A．
点评：本题考查参数方程与普通方程的互化及直线与圆相切，充分利用直线与圆相切的充要条件是圆心到直线的距离等于半径是解决问题的关键．
练习册系列答案
相关题目
使
成立，则实数
的取值集合是__________．
，则线段CD的长为________．
：
（t为参数）与圆C2：
（
为参数）的位置关系不可能是________.
使
成立，则实数
的取值集合是__________．
，则线段CD的长为________．
：
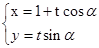（t为参数）与圆C2：
（
为参数）的位置关系不可能是________.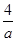
，对任意的x∈R恒成立，则实数a的取值范围是
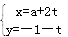（t为参数），圆C∶r=2
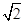cos(q―
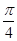)（极轴与x轴的非负半轴重合，且单位长度相同），若直线l被圆C截得弦长为2，则a=
，（t为参数）与圆
，（θ为参数）相切，则b=（ ）