Question

甲班有2名男乒乓球选手和3名女乒乓球选手，乙班有3名男乒乓球选手和1名女乒乓球选手，学校计划从甲乙两班各选2名选手参加体育交流活动．
（Ⅰ）求选出的4名选手均为男选手的概率．
（Ⅱ）记X为选出的4名选手中女选手的人数，求X的分布列和期望．

Answer 1

解：（Ⅰ）事件A表示“选出的4名选手均为男选手”．
由题意知…（3分）
=．…（5分）
（Ⅱ）X的可能取值为0，1，2，3．…（6分）
，…（7分）
，…（9分）
，…（10分）
P（X=2）=1-P（X=0）-P（X=1）-P（X=3）=．…（11分）
所以X的分布列：

X	0	1	2	3
P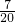

…（12分）
所以．…（13分）
分析：（I）根据题意可得：选出的4名选手均为男选手即甲乙两班各选2名男选手，共有C₃²中选法，进而得到答案．
（II）X的可能取值为0，1，2，3，再利用等可能事件的概率分别计算出其发生的概率，进而得到X的分布列与期望．
点评：本题主要考查离散型随机变量的分布列与期望，以及等可能事件的概率．