题目内容
若
，则x取值范围是 ．
【答案】分析：将原不等式转化为：若
，再利用指数函数的单调性可得|x+1|-|x-1|
，再分类讨论按照绝对值不等式求解．
解答：解：原不等式转化为：若
由指数函数的单调性得：|x+1|-|x-1|
①当x≤-1时，-2≥
不成立
②当-1＜x＜1时，原不等式转化为：2x≥
解得：x≥
③当x≥1时，原不等式转化为：2≥
成立
综上：x≥
故答案为：x≥
点评：本题主要考查绝对值不等式的解法和指数函数的单调性，属中档题．
，再利用指数函数的单调性可得|x+1|-|x-1|，再分类讨论按照绝对值不等式求解．解答：解：原不等式转化为：若
由指数函数的单调性得：|x+1|-|x-1|
①当x≤-1时，-2≥
不成立②当-1＜x＜1时，原不等式转化为：2x≥
解得：x≥
③当x≥1时，原不等式转化为：2≥
成立
综上：x≥
故答案为：x≥
点评：本题主要考查绝对值不等式的解法和指数函数的单调性，属中档题．
练习册系列答案
期末100分闯关海淀考王系列答案
相关题目
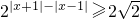，则x取值范围是 ________．