题目内容
4.若函数f(x)=loga(-x2+ax-1)(a>0且a≠1)有最大值,则实数a的取值范围是a>2.分析 若函数f(x)=loga(-x2+ax-1)(a>0且a≠1)有最大值,则外函数为增函数,且内函数的最大值为正,进而得到答案.
解答 解:若函数f(x)=loga(-x2+ax-1)(a>0且a≠1)有最大值,
则$\left\{\begin{array}{l}a>1\\ \frac{4-{a}^{2}}{-4}>0\end{array}\right.$,
解得:a>2,
故答案为:a>2.
点评 本题考查的知识点是对数函数的图象与性质,熟练掌握对数函数的图象和性质是解答的关键.

练习册系列答案
相关题目
14.下列命题中错误的是( )
| A. | 命题“若x2-5x+6=0则x=2”的逆否命题是“若x≠2则x2-5x+6≠0” | |
| B. | 命题“已知x、y∈R,若x+y≠3,则x≠2或y≠1是真命题” | |
| C. | 已知命题p和q,若p∨q为真命题,则命题p与q中必一真一假 | |
| D. | 命题p:?x0∈R,x02+x0+1<0,则¬p:?x0∈R,x02+x0+1≥0 |
12.幂函数y=f(x)的图象经过点A(2,4),则曲线y=f(x)在点A处切线的斜率为( )
| A. | 4 | B. | -4 | C. | 2 | D. | -2 |
14.某地区今年1月,2月,3月,4月,5月患某种传染病的人数分别是52,61,68,74,78.若用下列四个函数模型预测以后各月的患该种传染病的人数,哪个最不合理?( )
| A. | f(x)=kx+h | B. | f(x)=ax2+bx+c | C. | f(x)=pqx+r | D. | f(x)=mlnx+n |
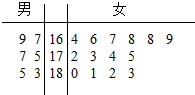 某航空公司在2015年年初招收了20名空乘人员(服务员与空警),其中“男性空乘人员”6名,“女性空乘人员”14名,并对他们的身高进行了测量,其身高(单位:cm)的茎叶图如图所示.公司决定:身高在170以上(包含170cm)的进入“国际航班”做空乘人员,身高在170cm以下的进入“国内航班”做空乘人员.
某航空公司在2015年年初招收了20名空乘人员(服务员与空警),其中“男性空乘人员”6名,“女性空乘人员”14名,并对他们的身高进行了测量,其身高(单位:cm)的茎叶图如图所示.公司决定:身高在170以上(包含170cm)的进入“国际航班”做空乘人员,身高在170cm以下的进入“国内航班”做空乘人员.



