题目内容
已知点A在直线2x+3y-6=0上运动,另一点B在圆(x+1)2+y2=1上运动,则|AB|的最小值为 .
考点:直线与圆的位置关系
专题:直线与圆
分析:由圆的方程,找出圆心坐标与半径r,利用点到直线的距离公式求出圆心到直线2x+3y-6=0的距离d,|AB|的最小值即为d-r的值,求出即可.
解答:
解:由圆的方程得:圆心(-1,0),半径r=1,
∵圆心(-1,0)到直线2x+3y-6=0的距离d=
=
,
∴|AB|=d-r=
-1,
故答案为:
-1.
∵圆心(-1,0)到直线2x+3y-6=0的距离d=
| |-2-6| | ||
|
8
| ||
| 13 |
∴|AB|=d-r=
8
| ||
| 13 |
故答案为:
8
| ||
| 13 |
点评:此题考查了直线与圆的位置关系,直线与圆的位置关系由d与r的大小来判断,当d=r时,直线与圆相切;当d<r时,直线与圆相交;当d>r时,直线与圆相离.

练习册系列答案
相关题目
在四边形ABCD中,
-
+
等于( )
| AB |
| AC |
| BD |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2.
如图,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2.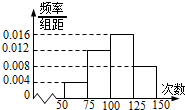 为了了解初中生的身体素质,某地区随机抽取了n名学生进行跳绳测试,根据所得数据画样本的频率分布直方图如图所示,且从左到右第一小组的频数是10,则n的值为
为了了解初中生的身体素质,某地区随机抽取了n名学生进行跳绳测试,根据所得数据画样本的频率分布直方图如图所示,且从左到右第一小组的频数是10,则n的值为