题目内容
某同学用“五点法”画函数 在某一个周期内的图象时,列表并填入的部分数据如下表:
在某一个周期内的图象时,列表并填入的部分数据如下表:| x | ______ |  | ______ |  | ______ |
| ωx+φ |  | π |  | 2π | |
| Asin(ωx+φ) | 2 | -2 |
(2)当
 时,求函数f(x)的值域.
时,求函数f(x)的值域.
【答案】分析:(1)由题意通过函数的周期,直接填表即可.
(2)通过x的范围,求出函数的表达式相位的范围,然后求出函数的值域的范围即可.
解答:解:(1)由题意得T=2( )=π.所以表中数据如下:
)=π.所以表中数据如下:
∴f(x)=2sin(2x- ).
).
(2)因为 ,
,
所以 ,
,
∴sin(2x- )
) ,
,
2sin(2x- )
) .
.
∴函数f(x)的值域为 .
.
故答案为: ;
; ;
; .
.
点评:本题考查三角函数的解析式的求法,函数的周期,函数的值域的求法,考查计算能力.
(2)通过x的范围,求出函数的表达式相位的范围,然后求出函数的值域的范围即可.
解答:解:(1)由题意得T=2(
 )=π.所以表中数据如下:
)=π.所以表中数据如下:| x |  |  |  |  |  |
| ωx+φ |  | π |  | 2π | |
| Asin(ωx+φ) | 2 | -2 |
 ).
).(2)因为
 ,
,所以
 ,
,∴sin(2x-
 )
) ,
,2sin(2x-
 )
) .
.∴函数f(x)的值域为
 .
.故答案为:
 ;
; ;
; .
.点评:本题考查三角函数的解析式的求法,函数的周期,函数的值域的求法,考查计算能力.

练习册系列答案
相关题目
某同学用“五点法”画函数y=Asin(ωx+φ)(A>0,ω>0)在一个周期内简图时,列表如下:
|
某同学用“五点法”画函数y=Asin(ωx+φ)(A>0,ω>0)在一个周期内简图时,列表如下:
则有( )
A.A=0,ω=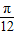 ,φ=0
,φ=0
B.A=2,ω=3,φ=
C.A=2,ω=3,φ=-
D.A=1,ω=2,φ=-
| ωx+φ |  | π |  | 2π | |
| x |  |  |  |  |  |
| y | 2 | -2 |
A.A=0,ω=
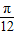 ,φ=0
,φ=0B.A=2,ω=3,φ=

C.A=2,ω=3,φ=-

D.A=1,ω=2,φ=-
