题目内容
【题目】对数列![]() ,规定
,规定![]() 为数列
为数列![]() 的一阶差分数列,其中
的一阶差分数列,其中![]() ,规定
,规定![]() 为
为![]() 的二阶差分数列,其中
的二阶差分数列,其中![]() .
.
(1)数列![]() 的通项公式
的通项公式![]() ,试判断
,试判断![]() ,
,![]() 是否为等差数列,请说明理由?
是否为等差数列,请说明理由?
(2)数列![]() 是公比为
是公比为![]() 的正项等比数列,且
的正项等比数列,且![]() ,对于任意的
,对于任意的![]() ,都存在
,都存在![]() ,使得
,使得![]() ,求
,求![]() 所有可能的取值构成的集合;
所有可能的取值构成的集合;
(3)各项均为正数的数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,对满足
,对满足![]() ,
,![]() 的任意正整数
的任意正整数![]() 、
、![]() 、
、![]() ,都有
,都有![]() ,且不等式
,且不等式![]() 恒成立,求实数
恒成立,求实数![]() 的最大值.
的最大值.
【答案】(1)![]() ,
,![]() 是等差数列,见解析(2)
是等差数列,见解析(2)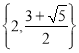 ;(3)2
;(3)2
【解析】
(1)根据题干中的定义,结合等差数列的定义即可判断.
(2)根据等比数列的通项公式可得![]() ,结合题干可得
,结合题干可得![]() ,从而可得
,从而可得![]() ,且
,且![]() ;分类讨论
;分类讨论![]() 、
、![]() 或
或![]() 即可求出
即可求出![]() .
.
(3)根据题中对数列的定义可得![]()
![]() ,从而可得
,从而可得![]() ,即
,即![]() 是等差数列,根据数列为正项等差数列可得
是等差数列,根据数列为正项等差数列可得![]() ,代入等差数列前
,代入等差数列前![]() 项和公式,由
项和公式,由![]() ,可得
,可得![]() ,当
,当![]() 时,不等式
时,不等式![]() 都成立;当
都成立;当![]() 时,令
时,令![]() ,
,![]() ,代入等差数列的前
,代入等差数列的前![]() 项和公式,作差
项和公式,作差![]() ,由
,由![]() ,
,![]() ,即可求解.
,即可求解.
解:(1)因为![]() ,所以
,所以![]() ,
,
则![]() ,又
,又![]() ,所以
,所以![]() 是首项为3,公差为2的等差数列.
是首项为3,公差为2的等差数列.
因为![]() ,则
,则![]() 是首项为2,公差为0的等差数列.
是首项为2,公差为0的等差数列.
(2)因为数列![]() 是公比为
是公比为![]() 的正项等比数列,所以
的正项等比数列,所以![]() .
.
又![]() ,
,
且对任意的![]() ,都存在
,都存在![]() ,使得
,使得![]() ,
,
所以对任意的![]() ,都存在
,都存在![]() ,使得
,使得![]() ,
,
即![]() ,因为
,因为![]() ,所以
,所以![]() .
.
![]() 若
若![]() ,则
,则![]() ,解得
,解得![]() (舍)或
(舍)或![]() ,
,
即当![]() 时,对任意的
时,对任意的![]() ,都有
,都有![]() .
.
![]() 若
若![]() ,则
,则![]() ,解得
,解得![]() (舍)或
(舍)或![]() ,
,
即当![]() 时,对任意的
时,对任意的![]() ,都有
,都有![]() .
.
![]() 若
若![]() ,则
,则![]() ,
,
故对任意的![]() ,不存在
,不存在![]() ,使得
,使得![]() .
.
综上所述,![]() 所有可能的取值构成的集合为
所有可能的取值构成的集合为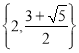 ;
;
(3)因为![]() ,所以
,所以![]()
![]() ,
,
则![]() ,所以
,所以![]() 是等差数列.
是等差数列.
设![]() 的公差为
的公差为![]() ,则
,则![]() .
.
若![]() ,则
,则![]() ;
;
若![]() ,则当
,则当![]() 时,
时,![]() ,
,
与数列![]() 的各项均为正数矛盾,故
的各项均为正数矛盾,故![]() .
.
由等差数列前![]() 项和公式可得
项和公式可得![]() ,
,
所以![]()
![]() ,
,
![]() ,
,
又![]() ,
,![]() ,
,
所以![]()
![]() ,
,
则当![]() 时,不等式
时,不等式![]() 都成立.
都成立.
另一方面,当![]() 时,令
时,令![]() ,
,![]() ,
,
则![]()
![]() ,
,
![]() ,
,
则![]()
![]() ,
,
因为![]() ,
,![]() ,
,
所以当![]() 时,
时,![]() ,即
,即![]() .不满足任意性.
.不满足任意性.
所以![]() .
.
综上,![]() 的最大值为2.
的最大值为2.

【题目】2020年春,新型冠状病毒在我国湖北武汉爆发并讯速蔓延,病毒传染性强并严重危害人民生命安全,国家卫健委果断要求全体人民自我居家隔离,为支援湖北武汉新型冠状病毒疫情防控工作,各地医护人员纷纷逆行,才使得病毒蔓延得到了有效控制.某社区为保障居民的生活不受影响,由社区志愿者为其配送蔬菜、大米等生活用品,记者随机抽查了男、女居民各100名对志愿者所买生活用品满意度的评价,得到下面的2×2列联表.
特别满意 | 基本满意 | |
男 | 80 | 20 |
女 | 95 | 5 |
(1)被调查的男性居民中有5个年轻人,其中有2名对志愿者所买生活用品特别满意,现在这5名年轻人中随机抽取3人,求至多有1人特别满意的概率.
(2)能否有99%的把握认为男、女居民对志愿者所买生活用品的评价有差异?
附: 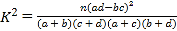
|
|
|
|
|
|
|
|