题目内容
15.已知函数f(x)=$\sqrt{{x^2}-ax+3a}$,对于任意x≥2,当△x>0时,恒有f(x+△x)>f(x),则实数a的取值范围是[-4,4].分析 由题意可得函数单调递增,结合图象可得$\left\{\begin{array}{l}{x=-\frac{-a}{2×1}≤2}\\{{2}^{2}-2a+3a≥0}\end{array}\right.$,解关于a的不等式组可得.
解答 解:∵函数f(x)=$\sqrt{{x^2}-ax+3a}$,对于任意x≥2,当△x>0时,恒有f(x+△x)>f(x),
∴函数f(x)=$\sqrt{{x^2}-ax+3a}$在x≥2时单调递增,
∴$\left\{\begin{array}{l}{x=-\frac{-a}{2×1}≤2}\\{{2}^{2}-2a+3a≥0}\end{array}\right.$,解得-4≤a≤4
故答案为:[-4,4]
点评 本题考查函数的单调性和恒成立问题,转化为二次函数的单调性是解决问题的关键,属中档题.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
6.已知为虚数单位,复数z满足z=$\frac{1+i}{1-i}$,则z2=( )
| A. | 1 | B. | -1 | C. | 2i | D. | -2i |
3.袋中装有5个同样大小的球,编号为1,2,3,4,5.现从该袋内随机取出3个球,记被取出的球的最大号码数为ξ,则Eξ等于( )
| A. | 4 | B. | 4.5 | C. | 4.75 | D. | 5 |
4.设等比数列{an}的通项为an=$\frac{1}{n(n+1)}$,则其前10项的和S10等于( )
| A. | $\frac{9}{10}$ | B. | $\frac{11}{10}$ | C. | $\frac{10}{9}$ | D. | $\frac{10}{11}$ |
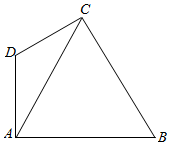 滨湖区拟建一主题游戏园,该游戏园为四边形区域ABCD,其中三角形区城ABC为主题活动区,其中∠ACB=60°,∠ABC=45°,AB=12$\sqrt{6}$m;AD、CD为游客通道(不考虑宽度),且∠ADC=120°,通道AD、CD围成三角形区域ADC为游客休闲中心,供游客休憩.
滨湖区拟建一主题游戏园,该游戏园为四边形区域ABCD,其中三角形区城ABC为主题活动区,其中∠ACB=60°,∠ABC=45°,AB=12$\sqrt{6}$m;AD、CD为游客通道(不考虑宽度),且∠ADC=120°,通道AD、CD围成三角形区域ADC为游客休闲中心,供游客休憩.