题目内容
同时具有下列性质:“①对任意x∈R,f(x+π)=f(x)恒成立;②图象关于直线 对称;③函数在
对称;③函数在 上是增函数的函数可以是
上是增函数的函数可以是
- A..
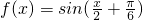
- B.

- C..

- D.
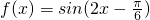
D
分析:由题意设出函数的表达式,求出函数的周期,确定ω的值,利用对称性,结合在 上是增函数确定选项即可.
上是增函数确定选项即可.
解答:由选项可知函数的解析式设为y=sin(ωx+φ)或y=cos(ωx+φ);
①对任意x∈R,f(x+π)=f(x)恒成立;周期为π,ω=2;排除A;
②图象关于直线x= 对称;所以B不正确,D、C正确;
对称;所以B不正确,D、C正确;
③函数在 上是增函数所以D正确;f(x)=cos(2x+
上是增函数所以D正确;f(x)=cos(2x+ )是减函数,C不正确;
)是减函数,C不正确;
故选:D.
点评:本题是考查三角函数的解析式的确定,通过函数的已知的性质确定表达式,考查计算能力,推理能力.解决本题用的是一一排除法,解决本题的关键在于熟练掌握三角函数的性质.
分析:由题意设出函数的表达式,求出函数的周期,确定ω的值,利用对称性,结合在
 上是增函数确定选项即可.
上是增函数确定选项即可.解答:由选项可知函数的解析式设为y=sin(ωx+φ)或y=cos(ωx+φ);
①对任意x∈R,f(x+π)=f(x)恒成立;周期为π,ω=2;排除A;
②图象关于直线x=
 对称;所以B不正确,D、C正确;
对称;所以B不正确,D、C正确;③函数在
 上是增函数所以D正确;f(x)=cos(2x+
上是增函数所以D正确;f(x)=cos(2x+ )是减函数,C不正确;
)是减函数,C不正确;故选:D.
点评:本题是考查三角函数的解析式的确定,通过函数的已知的性质确定表达式,考查计算能力,推理能力.解决本题用的是一一排除法,解决本题的关键在于熟练掌握三角函数的性质.

练习册系列答案
 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
同时具有下列性质:“①对任意x∈R,f(x+π)=f(x)恒成立;②图象关于直线x=
对称”的函数可以是( )
| π |
| 3 |
A、f(x)=sin(
| ||||
B、f(x)=sin(2x-
| ||||
C、f(x)=cos(2x-
| ||||
D、f(x)=cos(2x+
|
对任意x∈R,函数f(x)同时具有下列性质:①f(x+π)=f(x);②f(
+x)=f(
-x),则函数f(x)可以是( )
| π |
| 3 |
| π |
| 3 |
A、f(x)=sin(
| ||||
B、f(x)=sin(2x-
| ||||
C、f(x)=cos(2x-
| ||||
D、f(x)=cos(2x-
|
对任意x∈R,函数f(x)同时具有下列性质:①f(x+π)=f(x);②函数f(x)的一条对称轴是x=
,则函数f(x)可以是( )
| π |
| 3 |
A、f(x)=sin(
| ||||
B、f(x)=sin(2x-
| ||||
C、f(x)=cos(2x-
| ||||
D、f(x)=cos(2x-
|