题目内容
【题目】在几何体![]() 中,
中,![]() 面
面![]() ,直角梯形
,直角梯形![]() 中,
中,![]() ,
,![]() ,且
,且![]() ,且
,且![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)若直线![]() 与平面
与平面![]() 所成角的正切值为
所成角的正切值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析(2)![]()
【解析】
(1)过点![]() 作
作![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,根据勾股定理的逆定理可知,
,根据勾股定理的逆定理可知,![]() ,由
,由![]() 面
面![]() 可得
可得![]() ,根据线面垂直的判定定理可证得
,根据线面垂直的判定定理可证得![]() 平面
平面![]() ,再由面面垂直的判定定理即可证出;
,再由面面垂直的判定定理即可证出;
(2)易证![]() 面
面![]() ,可得
,可得![]() 为
为![]() 与面
与面![]() 所成的角,从而可计算出
所成的角,从而可计算出![]() ,再以
,再以![]() 为原点,分别以
为原点,分别以![]() ,
,![]() 与
与![]() 为
为![]() 轴,建立空间直角坐标系,然后分别求出平面
轴,建立空间直角坐标系,然后分别求出平面![]() 的法向量和平面
的法向量和平面![]() 的法向量,即可由向量法求出二面角
的法向量,即可由向量法求出二面角![]() 的余弦值.
的余弦值.
(1)如图所示: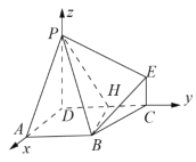
∵![]() 面
面![]() ,∴
,∴![]() ,
,
在梯形![]() 中,过
中,过![]() 作
作![]() 交
交![]() 于
于![]() ,∴
,∴![]() ,
,![]() ,
,![]() ,∴
,∴![]() ,即
,即![]() ,即
,即![]() .
.
∵![]() ,
,![]() ,∴
,∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ∴平面
∴平面![]() 平面
平面![]() ,
,
(2)连接![]() ,
,![]() 面
面![]() ,∴
,∴![]() 为
为![]() 与面
与面![]() 所成的角,
所成的角,![]() ,∵
,∵![]() ,∴
,∴![]() ,∵
,∵![]() ,
,![]() ,∴
,∴![]() ,
,
以![]() 为原点,分别以
为原点,分别以![]() ,
,![]() 与
与![]() 为
为![]() 轴,建立如图所示的空间直角坐标系,则
轴,建立如图所示的空间直角坐标系,则![]() ,可知
,可知![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
可知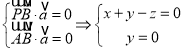 ,可取
,可取![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
可知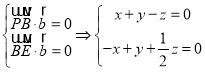 ,可取
,可取![]() ,
,
可知两向量的夹角的余弦值为![]() .
.
由图可知二面角![]() 为钝角,所以二面角
为钝角,所以二面角![]() 的余弦值为
的余弦值为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某手机生产企业为了对研发的一批最新款手机进行合理定价,将该款手机按事先拟定的价格进行试销,得到单价![]() (单位:千元)与销量
(单位:千元)与销量![]() (单位:百件)的关系如下表所示:
(单位:百件)的关系如下表所示:
单价 | 1 | 1.5 | 2 | 2.5 | 3 |
销量 | 10 | 8 | 7 | 6 |
|
已知![]() .
.
(Ⅰ)若变量![]() ,
,![]() 具有线性相关关系,求产品销量
具有线性相关关系,求产品销量![]() (百件)关于试销单价
(百件)关于试销单价![]() (千元)的线性回归方程
(千元)的线性回归方程![]() ;
;
(Ⅱ)用(Ⅰ)中所求的线性回归方程得到与![]() 对应的产品销量的估计值
对应的产品销量的估计值![]() ,当销售数据
,当销售数据![]() 对应的残差满足
对应的残差满足![]() 时,则称
时,则称![]() 为一个“好数据”,现从5个销售数据中任取3个,求其中“好数据”的个数
为一个“好数据”,现从5个销售数据中任取3个,求其中“好数据”的个数![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式: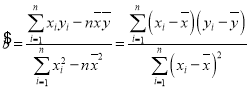 ,
,![]() .
.