题目内容
已知ab≠0，求证：a＋b＝1的充要条件是a3＋b3＋ab－a2－b2＝0.
证明 充分性：∵a3＋b3＋ab－a2－b2
＝(a＋b)(a2－ab＋b2)－(a2－ab＋b2)
＝(a
＋b－1)(a2－ab＋b2)
∴(a＋b－1)(a2－ab＋b2)＝0.
又ab≠0，即a≠0且b≠0，
∴a2－ab－b2＝
＋
b2>0.
∴a＋b－1＝0，∴a＋b＝1.
必要性：∵a＋b＝1，即a＋b－1＝0，
∴a3＋b3＋ab－a2－b2
＝(a＋b－1)(a2－ab＋b2)＝0.
综上可知，当ab≠0时，
a＋b＝1的充要条件是a3＋b3＋ab－a2－b2＝0.
练习册系列答案
名校课堂系列答案
相关题目
”的推理过程中，其大前提是______________．
；
_条件．
|x－2|<3的否命题与逆否命题；
，焦点是(－3,0)，(3,0)，则椭圆方程为
______________．
)是椭圆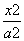
＋
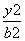＝1 (a>b>0)上的一点，F1、F2为椭圆的两焦点，若PF1⊥PF2，试求：
________.