题目内容
设椭圆E中心在原点,焦点在x轴上,短轴长为4,点M(2,
)在椭圆上.
(1)求椭圆E的方程;
(2)设动直线L交椭圆E于A、B两点,且
⊥
,求△OAB的面积的取值范围.
| 2 |
(1)求椭圆E的方程;
(2)设动直线L交椭圆E于A、B两点,且
| OA |
| OB |
分析:(1)设出椭圆方程,确定b的值,代入M的坐标,即可求得椭圆的方程;
(2)分类讨论,设出直线方程,代入椭圆方程,利用韦达定理,及使
⊥
,需使x1x2+y1y2=0,表示出三角形的面积,进而可得△OAB的面积的取值范围.
(2)分类讨论,设出直线方程,代入椭圆方程,利用韦达定理,及使
| OA |
| OB |
解答:解:(1)椭圆方程为
+
=1(a>b>0),则b=2
将点M(2,
),代入椭圆方程可得
+
=1,∴a2=8
∴椭圆方程为
+
=1;
(2)当直线L斜率存在时,设方程为y=kx+m,代入椭圆方程,可得(1+2k2)x2+4kmx+2m2-8=0
则△=8(8k2-m2+4)>0,即8k2-m2+4>0(*),
设A(x1,y1),B(x2,y2),则x1+x2=-
,x1x2=
∴y1y2=(kx1+m)(kx2+m)=
要使
⊥
,需使x1x2+y1y2=0,即
+
=0,所以m2=
①
将它代入(*)式可得k2∈[0,+∞)
∵O到L的距离为d=
∴S=
|AB|d=
|x1-x2|•
=
|m||x1-x2|=
①当k=0时,S=
;
②当AB的斜率不存在时,S=
;
③当k≠0时,S=
∵k2∈(0,+∞),∴4k2+
∈[4,+∞),∴S∈(
,2
]
综上,S∈[
,2
].
| x2 |
| a2 |
| y2 |
| b2 |
将点M(2,
| 2 |
| 4 |
| a2 |
| 2 |
| 4 |
∴椭圆方程为
| x2 |
| 8 |
| y2 |
| 4 |
(2)当直线L斜率存在时,设方程为y=kx+m,代入椭圆方程,可得(1+2k2)x2+4kmx+2m2-8=0
则△=8(8k2-m2+4)>0,即8k2-m2+4>0(*),
设A(x1,y1),B(x2,y2),则x1+x2=-
| 4km |
| 1+2k2 |
| 2m2-8 |
| 1+2k2 |
∴y1y2=(kx1+m)(kx2+m)=
| m2-8k2 |
| 1+2k2 |
要使
| OA |
| OB |
| 2m2-8 |
| 1+2k2 |
| m2-8k2 |
| 1+2k2 |
| 8k2+8 |
| 3 |
将它代入(*)式可得k2∈[0,+∞)
∵O到L的距离为d=
| |m| | ||
|
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1+k2 |
| |m| | ||
|
| 1 |
| 2 |
| 8 |
| 3 |
1+
|
①当k=0时,S=
| 8 |
| 3 |
②当AB的斜率不存在时,S=
| 8 |
| 3 |
③当k≠0时,S=
| 8 |
| 3 |
1+
|
∵k2∈(0,+∞),∴4k2+
| 1 |
| k2 |
| 8 |
| 3 |
| 2 |
综上,S∈[
| 8 |
| 3 |
| 2 |
点评:本题考查椭圆的方程,考查直线与椭圆的位置关系,考查分类讨论的数学思想,考查学生分析解决问题的能力,有难度.

练习册系列答案
相关题目
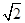 )在椭圆上,。
)在椭圆上,。 ,求△OAB的面积的取值范围。
,求△OAB的面积的取值范围。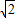 )在椭圆上.
)在椭圆上.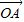
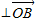 ,求△OAB的面积的取值范围.
,求△OAB的面积的取值范围.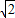 )在椭圆上.
)在椭圆上.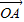
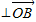 ,求△OAB的面积的取值范围.
,求△OAB的面积的取值范围.