题目内容
(本小题满分13分) 设椭圆E中心在原点,焦点在x轴上,短轴长为4,点M(2,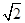 )在椭圆上,。
)在椭圆上,。
(1)求椭圆E的方程;
(2)设动直线L交椭圆E于A、B两点,且 ,求△OAB的面积的取值范围。
,求△OAB的面积的取值范围。
【答案】
(1) ;(2)S
;(2)S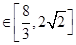 。
。
【解析】
试题分析:(1)因为椭圆E: 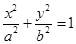 (a>b>0)过M(2,
(a>b>0)过M(2,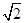 ) ,2b=4
) ,2b=4
故可求得b=2,a=2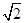 椭圆E的方程为
椭圆E的方程为 ……2分
……2分
(2)设A(x1,y1),B(x2,y2),当直线L斜率存在时设方程为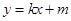 ,
,
解方程组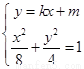 得
得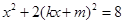 ,即
,即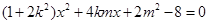 ,
,
则△=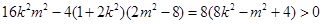 ,
,
即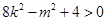 (*)……………………4分
(*)……………………4分
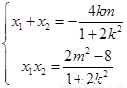 ,
,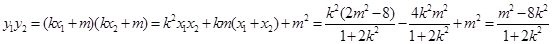 要使
要使 ,需使
,需使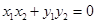 ,即
,即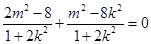 ,
,
所以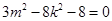 , 即
, 即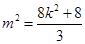 ①………………………7分
①………………………7分
将它代入(*)式可得 ……………………………8分
……………………………8分
P到L的距离为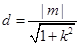
又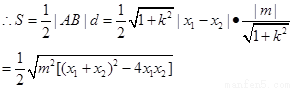
将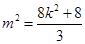 及韦达定理代入可得
及韦达定理代入可得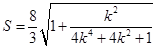 ……………………10分
……………………10分
当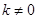 时
时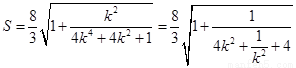
由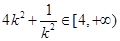 故
故 ……………12分
……………12分
当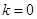 时,
时, 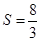
当AB的斜率不存在时, 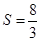 ,
,
综上S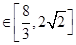 ……………………………13分
……………………………13分
考点:本题主要考查椭圆标准方程,直线与椭圆的位置关系。
点评:求椭圆的标准方程是解析几何的基本问题,涉及直线与椭圆的位置关系问题,常常运用韦达定理,本题属于中档题。

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目

 .
. 的最小正周期和最大值;
的最小正周期和最大值; 在区间
在区间 上的图象.
上的图象. ,且方程
,且方程 有两个不同的实数根,求实数m的取值范围.
有两个不同的实数根,求实数m的取值范围. 的函数
的函数 是奇函数.
是奇函数. 的值;(2)判断函数
的值;(2)判断函数 的单调性;
的单调性; ,不等式恒成立
,不等式恒成立 ,求k的取值范围.
,求k的取值范围. ,
,  ,
, .
. (∁
(∁ ; (2)若
; (2)若 ,求
,求 的取值范围.
的取值范围. 的所有棱长都为2,
的所有棱长都为2, 为
为 的中点。
的中点。 ∥平面
∥平面 ;
; 所成的角。www.7caiedu.cn
所成的角。www.7caiedu.cn

 为锐角,且
为锐角,且 ,函数
,函数 ,数列{
,数列{ }的首项
}的首项 .
. 的表达式;
的表达式; 中,若
中,若 A=2
A=2 ,BC=2,求
,BC=2,求 的前
的前 项和
项和