题目内容
已知命题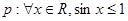 ,则( )
,则( )
A. | B. |
C. | D. |
C
解析试题分析:因为命题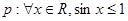 ,根据正弦函数的性质可知,显然成立。那么其否定即将任意,改为存在,得到
,根据正弦函数的性质可知,显然成立。那么其否定即将任意,改为存在,得到 ,同时结论
,同时结论 取其否定得到为
取其否定得到为 ,因此可知命题P的否定为
,因此可知命题P的否定为 ,选C.
,选C.
考点:本题主要考查了全称命题的否定的求解。
点评:解决该试题的关键是理解全称命题的否定是特称命题,同时要将任意改为存在,结论成立改为不成立取其否定形式,得到即为所求。

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
已知E,F,G,H是空间四点,命题甲:E,F,G,H四点不共面,命题乙:直线EF和GH不相交,则甲是乙的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
对于命题 和命题
和命题 ,“
,“ 为真命题”的必要不充分条件是( )
为真命题”的必要不充分条件是( )
A. 为假命题 为假命题 | B. 为假命题 为假命题 |
C. 为真命题 为真命题 | D. 为真命题 为真命题 |
命题“若 则
则 ”的逆否命题是( )
”的逆否命题是( )
A.若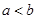 ,则 ,则 | B.若 ,则 ,则 |
C.若 ,则 ,则 | D.若 ,则 ,则 |
已知命题 :
: 命题
命题 :
:  则下列判断正确的是( )
则下列判断正确的是( )
A. 是真命题 是真命题 | B. 是假命题 是假命题 | C. 是假命题 是假命题 | D. q是假命题 q是假命题 |
“ ”是“
”是“ ”的( )
”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
若“ ,
, ”为真命题,则实数
”为真命题,则实数 的取值范围是( )
的取值范围是( )
A. | B.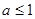 | C. | D. |
在实数集 中,我们定义的大小关系“
中,我们定义的大小关系“ ”为全体实数排了一个“序”,类似地,我们在复数集
”为全体实数排了一个“序”,类似地,我们在复数集 上也可以定义一个称为“序”的关系,记为“
上也可以定义一个称为“序”的关系,记为“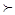 ”。定义如下:对于任意两个复数
”。定义如下:对于任意两个复数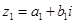 ,
, (
( ,
, 为虚数单位),“
为虚数单位),“ ”当且仅当“
”当且仅当“ ”或“
”或“ 且
且 ”.下面命题为假命题的是( )
”.下面命题为假命题的是( )
A.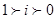 |
B.若 , , ,则 ,则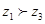 |
C.若 ,则对于任意 ,则对于任意 , ,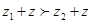 |
D.对于复数 ,若 ,若 ,则 ,则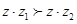 |
 中,若
中,若 ,则
,则 ;
; ,则
,则 在
在 上的投影为
上的投影为 ;
; ,
, ,则“
,则“ ”为假命题;
”为假命题;
 的导函数的最大值为
的导函数的最大值为 ,则函数
,则函数 的图
的图 对称.
对称.