题目内容
在平面直角坐标系xOy中,点P(a,b)(a>b>0)为动点,F1,F2分别为椭圆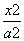 +
+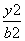 =1的左、右焦点,已知△F1PF2为等腰三角形.
=1的左、右焦点,已知△F1PF2为等腰三角形.
(1)求椭圆的离心率e;
(2)设直线PF2与椭圆相交于A,B两点,M是直线PF2上的点,满足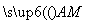 ·
·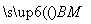 =-2,求点M的轨迹方程.
=-2,求点M的轨迹方程.
 由y=
由y= (x-c),得c=x-
(x-c),得c=x- y.
y.
于是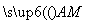 =
= ,
,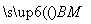 =(x,
=(x, x).
x).
由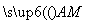 ·
·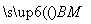 =-2,即
=-2,即 ·x+
·x+ ·
· x=-2,化简得18x2-16
x=-2,化简得18x2-16 xy-15=0,
xy-15=0,
将y= 代入c=x-
代入c=x- y,得c=
y,得c= >0.
>0.
所以x>0.
因此,点M的轨迹方程是18x2-16 xy-15=0(x>0).
xy-15=0(x>0).

练习册系列答案
相关题目
 B(2,0),点C、D满足
B(2,0),点C、D满足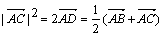
 离为
离为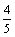 ,且l与D的轨迹相切,求椭圆方程.
,且l与D的轨迹相切,求椭圆方程. 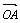 与
与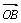 夹角的大小;
夹角的大小;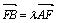 ,若λ∈[4,9],求l在y轴上截距的变化范围.
,若λ∈[4,9],求l在y轴上截距的变化范围.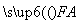 +
+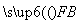 +
+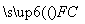 =0,且|
=0,且|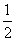 )作圆x2+y2=1的切线,切点分别为A,B,直线AB恰好经过椭圆的右焦点和上顶点,则椭圆方程是________________.
)作圆x2+y2=1的切线,切点分别为A,B,直线AB恰好经过椭圆的右焦点和上顶点,则椭圆方程是________________. )3+32(x-1) B.f(x)=2x+1
)3+32(x-1) B.f(x)=2x+1