题目内容
4. 如图,平面ABC⊥平面α,且平面ABC∩平面α=BC,AB=1,BC=$\sqrt{3}$,∠ABC=$\frac{5π}{6}$,平面α内一动点P满足∠PAB=$\frac{π}{6}$,则PC的最小值是$\frac{\sqrt{5}}{2}$.
如图,平面ABC⊥平面α,且平面ABC∩平面α=BC,AB=1,BC=$\sqrt{3}$,∠ABC=$\frac{5π}{6}$,平面α内一动点P满足∠PAB=$\frac{π}{6}$,则PC的最小值是$\frac{\sqrt{5}}{2}$.
分析 如图所示,建立空间直角坐标系,设P(x,y,0),可得$\overrightarrow{AP}•\overrightarrow{AB}$,可得$|\overrightarrow{PC}|$=$\sqrt{{x}^{2}+(y-\frac{\sqrt{3}}{2})^{2}+0}$.
解答 解:如图所示,建立空间直角坐标系,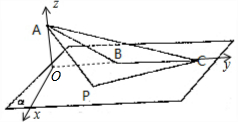
A$(0,0,\frac{1}{2})$,B$(0,\frac{\sqrt{3}}{2},0)$,C$(0,\frac{3\sqrt{3}}{2},0)$,设P(x,y,0),则$\overrightarrow{AP}$=$(x,y,-\frac{1}{2})$,$\overrightarrow{AB}$=$(0,\frac{\sqrt{3}}{2},-\frac{1}{2})$,
$\overrightarrow{AP}•\overrightarrow{AB}$=$\sqrt{{x}^{2}+{y}^{2}+(-\frac{1}{2})^{2}}$$•\sqrt{0+(\frac{\sqrt{3}}{2})^{2}+(-\frac{1}{2})^{2}}$$•cos\frac{π}{6}$,
∴$\frac{\sqrt{3}}{2}$y+$\frac{1}{4}$=$\sqrt{{x}^{2}+{y}^{2}+(-\frac{1}{2})^{2}}$$•cos\frac{π}{6}$,
∴$\frac{3}{4}{y}^{2}+\frac{\sqrt{3}}{4}$y+$\frac{1}{16}$=$\frac{3}{4}$$({x}^{2}+{y}^{2}+\frac{1}{4})$,
∴${x}^{2}=\frac{\sqrt{3}}{3}$y-$\frac{1}{6}$.
$|\overrightarrow{PC}|$=$\sqrt{{x}^{2}+(y-\frac{\sqrt{3}}{2})^{2}+0}$=$\sqrt{(y-\frac{\sqrt{3}}{3})^{2}+\frac{5}{4}}$≥$\frac{\sqrt{5}}{2}$,
∴PC的最小值是$\frac{\sqrt{5}}{2}$.
故答案为:$\frac{\sqrt{5}}{2}$.
点评 本题考查了空间位置关系、空间向量的应用、数量积运算性质,考查了推理能力与计算能力,属于中档题.

 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案| A. | {-1,0,1,2} | B. | {0,1,2} | C. | {-1,0,1,2,3} | D. | {0,1,2,3} |
| A. | 146石 | B. | 172石 | C. | 341石 | D. | 1358石 |
 的图像大致是( )
的图像大致是( )
 ,则
,则 等于( )
等于( ) B.
B. C.
C. D.
D.
 满足
满足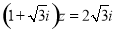 (
(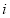 为虚数单位),则
为虚数单位),则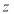 在复平面内对应的点位于( )
在复平面内对应的点位于( )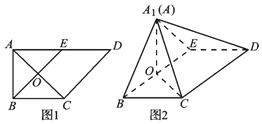 如图1,在直角梯形ABCD中,AD∥BC,∠BAD=$\frac{π}{2}$,AB=BC=1,AD=2,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到图22中△A1BE的位置,得到四棱锥A1-BCDE.
如图1,在直角梯形ABCD中,AD∥BC,∠BAD=$\frac{π}{2}$,AB=BC=1,AD=2,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到图22中△A1BE的位置,得到四棱锥A1-BCDE. 如图,三棱锥P-ABC中,PB⊥底面ABC,∠BCA=90°,PB=BC=CA=2,E为PC的中点,点F在PA上,且2PF=FA.
如图,三棱锥P-ABC中,PB⊥底面ABC,∠BCA=90°,PB=BC=CA=2,E为PC的中点,点F在PA上,且2PF=FA.