题目内容
已知向量
=(2sinx,-1),
=(cosx,cos2x),定义函数f(x)=
•
.
(Ⅰ)求函数f(x)的表达式,并指出其最大最小值;
(Ⅱ)在锐角△ABC中,角A,B,C的对边分别为a,b,c,且f(A)=1,bc=8,求△ABC的面积S.
| OP |
| OQ |
| OP |
| OQ |
(Ⅰ)求函数f(x)的表达式,并指出其最大最小值;
(Ⅱ)在锐角△ABC中,角A,B,C的对边分别为a,b,c,且f(A)=1,bc=8,求△ABC的面积S.
(Ⅰ)∵
=(2sinx,-1),
=(cosx,cos2x),
∴f(x)=
•
=2sinxcosx-cos2x=sin2x-cos2x=
sin(2x-
),
∵-1≤sin(2x-
)≤1,
∴f(x)的最大值为
,最小值为-
;
(Ⅱ)∵f(A)=1,
∴sin(2A-
)=
,
∴2A-
=
或2A-
=
,
∴A=
或A=
,又△ABC为锐角三角形,
则A=
,又bc=8,
则△ABC的面积S=
bcsinA=
×8×
=2
.
| OP |
| OQ |
∴f(x)=
| OP |
| OQ |
| 2 |
| π |
| 4 |
∵-1≤sin(2x-
| π |
| 4 |
∴f(x)的最大值为
| 2 |
| 2 |
(Ⅱ)∵f(A)=1,
∴sin(2A-
| π |
| 4 |
| ||
| 2 |
∴2A-
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
∴A=
| π |
| 4 |
| π |
| 2 |
则A=
| π |
| 4 |
则△ABC的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 2 |

练习册系列答案
相关题目
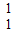 ],并且矩阵M对应的变换将点(-1,2)变换成(9,15),求矩阵M.
],并且矩阵M对应的变换将点(-1,2)变换成(9,15),求矩阵M.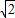 sin(
sin(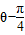 ),以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的参数方程为
),以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的参数方程为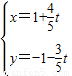 (t为参数),求直线l被曲线C所截得的弦长.
(t为参数),求直线l被曲线C所截得的弦长.
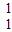 ],并且矩阵M对应的变换将点(-1,2)变换成(9,15),求矩阵M.
],并且矩阵M对应的变换将点(-1,2)变换成(9,15),求矩阵M.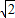 sin(
sin(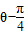 ),以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的参数方程为
),以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的参数方程为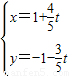 (t为参数),求直线l被曲线C所截得的弦长.
(t为参数),求直线l被曲线C所截得的弦长.
 与
与 的夹角θ的最大值.
的夹角θ的最大值.