题目内容
((本小题满分12分)设函数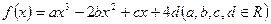 的图象关于原点对称,且
的图象关于原点对称,且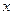 =1时,f(x)取极小值
=1时,f(x)取极小值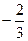 。
。
(1)求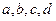 的值;
的值;
(2)若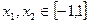 时,求证:
时,求证: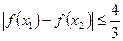 。
。
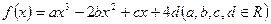 的图象关于原点对称,且
的图象关于原点对称,且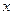 =1时,f(x)取极小值
=1时,f(x)取极小值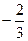 。
。(1)求
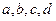 的值;
的值;(2)若
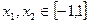 时,求证:
时,求证: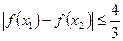 。
。解答(1) ∵函数f(x)图象关于原点对称,∴对任意实数x,都 有f(-x)="-" f(x).
有f(-x)="-" f(x).
∴-ax3-2bx2-cx+4d=-ax3+2bx2-cx-4d,即bx2-2d=0恒成立.
∴b=0,d=0,即f(x)=ax3+cx. ∴f′(x)=3ax2+c.
∵x=1时,f(x)取极小值- . ∴f′(1)=0且f(1)="-"
. ∴f′(1)=0且f(1)="-"  ,
,
即3a+c=0且a +c=-
+c=- . 解得a=
. 解得a=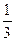 ,c=-1………………………………….6分
,c=-1………………………………….6分
(2)证明:∵f′(x)=x2-1,由f′(x)=0,得x=±1.
当x∈(-∞,-1)或(1,+∞)时,f′(x)>0; 当 x∈(-1,1)时,f′(x)<0.
∴f(x)在[-1,1]上是减函数,且fmax(x)=f(-1)= , fmin(x)=f(1)= -
, fmin(x)=f(1)= - .
.
∴在[-1,1]上,|f(x)|≤ .
.
于是x1,x2∈[-1,1]时,| f(x1)-f(x2)|≤
f(x1)-f(x2)|≤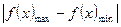 =
= +
+ =
=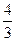 .
.
故x1,x2∈[-1,1 ]时,|f(x1)-f(x2)|≤
]时,|f(x1)-f(x2)|≤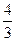 ………………………………………….12分
………………………………………….12分
 有f(-x)="-" f(x).
有f(-x)="-" f(x).∴-ax3-2bx2-cx+4d=-ax3+2bx2-cx-4d,即bx2-2d=0恒成立.
∴b=0,d=0,即f(x)=ax3+cx. ∴f′(x)=3ax2+c.
∵x=1时,f(x)取极小值-
 . ∴f′(1)=0且f(1)="-"
. ∴f′(1)=0且f(1)="-"  ,
,即3a+c=0且a
 +c=-
+c=- . 解得a=
. 解得a=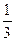 ,c=-1………………………………….6分
,c=-1………………………………….6分(2)证明:∵f′(x)=x2-1,由f′(x)=0,得x=±1.
当x∈(-∞,-1)或(1,+∞)时,f′(x)>0; 当 x∈(-1,1)时,f′(x)<0.
∴f(x)在[-1,1]上是减函数,且fmax(x)=f(-1)=
 , fmin(x)=f(1)= -
, fmin(x)=f(1)= - .
.∴在[-1,1]上,|f(x)|≤
 .
.于是x1,x2∈[-1,1]时,|
 f(x1)-f(x2)|≤
f(x1)-f(x2)|≤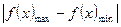 =
= +
+ =
=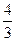 .
.故x1,x2∈[-1,1
 ]时,|f(x1)-f(x2)|≤
]时,|f(x1)-f(x2)|≤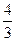 ………………………………………….12分
………………………………………….12分略

练习册系列答案
相关题目
 ,若
,若 ,求函数
,求函数 的单调区间与极值
的单调区间与极值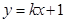 与曲线
与曲线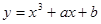 切于点(1, 3),则b的值为()
切于点(1, 3),则b的值为()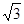
 分抛物线
分抛物线 与
与 轴所围成图形为面积相等的两部分,求
轴所围成图形为面积相等的两部分,求 的值。
的值。 
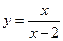 在点
在点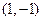 处的切线方程为
处的切线方程为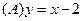
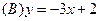
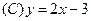
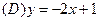
 在点
在点 处的切线方程为
处的切线方程为




 ,如果过点
,如果过点 可作曲线
可作曲线 的三条切线,则m的取值范围是
的三条切线,则m的取值范围是



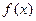 的定义域为开区间
的定义域为开区间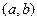 ,导函数
,导函数 在
在 图
图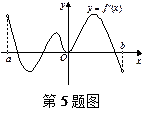

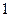 个 B
个 B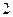 个 C
个 C 个 D
个 D