题目内容
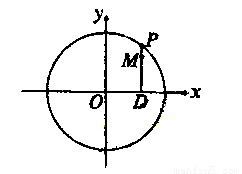
如图,设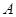 是圆
是圆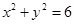 上的动点,点
上的动点,点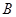 是
是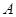 在
在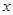 轴上投影,
轴上投影,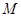 为
为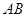 上一点,且
上一点,且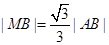 .当
.当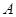 在圆上运动时,点
在圆上运动时,点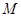 的轨迹为曲线
的轨迹为曲线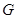 . 过点
. 过点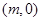
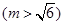 且倾斜角为
且倾斜角为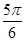 的直线
的直线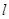 交曲线
交曲线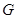 于
于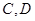 两点.
两点.
(1)求曲线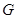 的方程;
的方程;
(2)若点F是曲线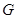 的右焦点且
的右焦点且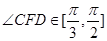 ,求
,求 的取值范围.
的取值范围.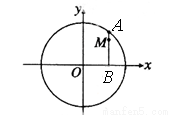
【答案】
(1)
(2)
【解析】
试题分析:解:(1)设点M的坐标是 ,
, 的坐标是
的坐标是 ,因为点
,因为点 是
是 在
在 轴上投影,M为
轴上投影,M为 上一点,且
上一点,且 ,所以
,所以 ,且
,且 ,∵
,∵ 在圆
在圆 上,∴
上,∴ ,整理得
,整理得 . 即
. 即 的方程是
的方程是 .
.
(2)如下图,直线 交曲线
交曲线 于
于 两点,且
两点,且 .
.

由题意得直线 的方程为
的方程为
 .
.
由 ,消去
,消去 得
得 .
.
由 解得
解得 .
.
又 ,
, .
.
设 ,则
,则 ,
,
 .
.
 .
.
 .
.
又由椭圆方程可知 ,
,
 ,
,
 ,
,
 ,
,
 .
.
因 ,
, ,
,
 ,故
,故 或
或 ,
,
又 ,故
,故 .
.
考点:直线与椭圆的位置关系
点评:主要是考查了椭圆方程以及直线与椭圆位置关系的联立方程设而不求的解题思想的运用,属于难度题。

练习册系列答案
相关题目
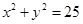 上的动点,点D是P在x轴上的
上的动点,点D是P在x轴上的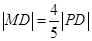
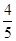 的直线被C所截线段的长度
的直线被C所截线段的长度 上的动点,点
上的动点,点 是
是 在
在 轴上的投影,
轴上的投影, 为线段PD上一点,且
为线段PD上一点,且 .点
.点 、
、 .
.
 轴上存在定点
轴上存在定点 ,使
,使 为定值,试求
为定值,试求 的最大值,并求此时点
的最大值,并求此时点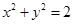 上的动点,点D是P在x轴上的投影。M为线段PD上一点,
上的动点,点D是P在x轴上的投影。M为线段PD上一点,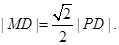
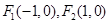 ,设点
,设点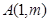
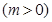 是轨迹C上的一点,求
是轨迹C上的一点,求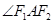 的
的 所在直线的方程。
所在直线的方程。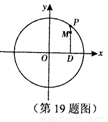
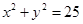 上的动点,点D是P在x轴上的射影,M为PD上一点,且
上的动点,点D是P在x轴上的射影,M为PD上一点,且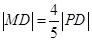
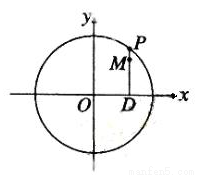
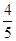 的直线被轨迹C所截线段的长度。
的直线被轨迹C所截线段的长度。