题目内容
是否存在常数k和等差数列{an},使kan2-1=S2n-Sn+1恒成立,其中Sn为{an}的前n项和?若存在,试求出常数k和数列{an}的通项;若不存在,试说明理由。
解:设存在常数k和等差数列{an}满足条件,
令an=pn+q(p,q为常数),
则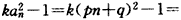
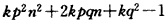 ,
,
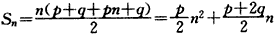 ,
,
∴S2n-Sn+1
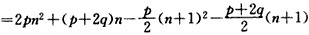
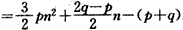 ,
,
由题设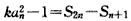 ,
,
得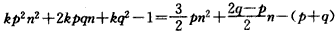 ,
,
上式对n∈N+恒成立,因而有
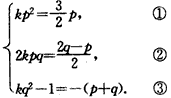
由①知,p=0或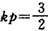 ,
,
若p=0,由②得q=0,不合题意,
∴p≠0,将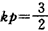 代入②,得
代入②,得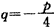 ,
,
代入③,得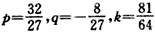 ,
,
∴存在常数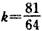 及等差数列{an}满足条件,{an}的通项公式为
及等差数列{an}满足条件,{an}的通项公式为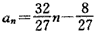 。
。
令an=pn+q(p,q为常数),
则
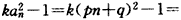
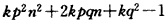 ,
,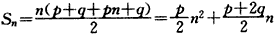 ,
,∴S2n-Sn+1
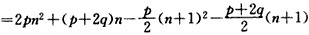
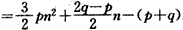 ,
,由题设
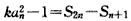 ,
,得
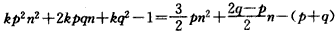 ,
,上式对n∈N+恒成立,因而有
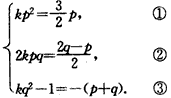
由①知,p=0或
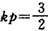 ,
,若p=0,由②得q=0,不合题意,
∴p≠0,将
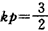 代入②,得
代入②,得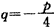 ,
,代入③,得
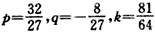 ,
,∴存在常数
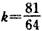 及等差数列{an}满足条件,{an}的通项公式为
及等差数列{an}满足条件,{an}的通项公式为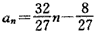 。
。 
练习册系列答案
相关题目
 ,求
,求 的值;
的值; 成立;
成立; 恒成立(n∈N*),若存在,试求出常数k和数列{an}的通项公式;若不存在,请说明理由。
恒成立(n∈N*),若存在,试求出常数k和数列{an}的通项公式;若不存在,请说明理由。 成立;
成立; -1=S2n-Sn+1恒成立(n∈N*),若存在,试求出常数k和数列{an}的通项公式;若不存在,请说明理由。
-1=S2n-Sn+1恒成立(n∈N*),若存在,试求出常数k和数列{an}的通项公式;若不存在,请说明理由。 成立;
成立; -1=S2n-Sn+1恒成立(n∈N*),若存在,试求出常数k和数列{an}的通项公式;若不存在,请说明理由。
-1=S2n-Sn+1恒成立(n∈N*),若存在,试求出常数k和数列{an}的通项公式;若不存在,请说明理由。