Question

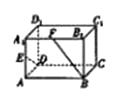
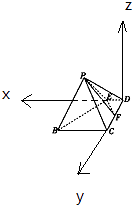
【题目】如图，E是矩形ABCD中AD边上的点，F是CD上的点，AB=AE= AD=4，现将△ABE沿BE边折至△PBE位置，并使平面PBE⊥平面BCDE，且平面PBE⊥平面PEF．

（1）求 的比值；
（2）求二面角E﹣PB﹣C的余弦值．

Answer 1

【答案】
（1）解：以D为原点，DE为x轴，DC为y轴，过D作平面BCDE的垂线为z轴，

建立空间直角坐标系，

P（4，2，2 ），B（6，4，0），E（2，0，0），设F（0，t，0），

=（2，2，﹣2 ）， =（﹣2，﹣2，﹣2 ）， =（﹣4，t﹣2，﹣2 ），

设平面PBE的法向量 =（x，y，z），

则 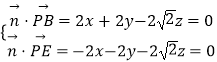，取x=1，得 =（1，﹣1，0），

设平面PEF的法向量 =（a，b，c），

则 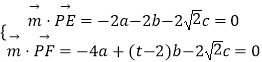，取b=2，得 =（t，2，﹣ ），

∵平面PBE⊥平面PEF，

∴ =t﹣2=0，解得t=2．

∴DF=2，FC=4﹣2=2，

∴ =1．

（2）解：C（0，4，0）， =（2，2，﹣2 ）， =（﹣4，2，﹣2 ），

设平面PBC的法向量 =（x1，y1，z1），

则 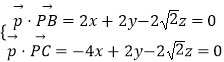，取y= ，得 =（0， ，1），

由（1）得平面PBE的法向量 =（1，﹣1，0），

cos＜ ＞= = =﹣ ，

由图形得二面角E﹣PB﹣C的平面角为锐角，

∴二面角E﹣PB﹣C的余弦值为 ．

【解析】（1）以D为原点，DE为x轴，DC为y轴，过D作平面BCDE的垂线为z轴，建立空间直角坐标系，利用向量法能求出 的比值．（2）求出平面PBC的法向量和平面PBE的法向量，利用向量法能求出二面角E﹣PB﹣C的余弦值．