题目内容
已知命题p:点P的坐标为(x,y),点F1、F2的坐标分别是(-1,0)、(1,0),命题q:直线PF1、PF2的斜率分别是k1、k2,k1•k2=m(m∈R),p∧q真.
(Ⅰ)求点P的轨迹方程;
(Ⅱ)指出点P的轨迹类型(如圆、抛物线、直线等).
(Ⅰ)求点P的轨迹方程;
(Ⅱ)指出点P的轨迹类型(如圆、抛物线、直线等).
分析:(Ⅰ)求出直线PF1、PF2的斜率,利用k1•k2=m,化简即可求点P的轨迹方程;
(Ⅱ)对m分类讨论,即可求得点P的轨迹类.
(Ⅱ)对m分类讨论,即可求得点P的轨迹类.
解答:解:(Ⅰ)由题意得,k1=
,k2=
,
∵k1•k2=m(m∈R),∴
•
=m,
所以所求轨迹方程是:mx2-y2=m(m∈R,x≠±1).…4分
(Ⅱ)由(Ⅰ)点P的轨迹方程为mx2-y2=m(m∈R,x≠±1),
当m<0且m≠-1时,方程可化为 x2+
=1(x≠±1),∴P的轨迹是椭圆(除去与x相交的项点);
当m=-1时,方程x2+y2=1(x≠±1),∴P的轨迹是圆(除去与x的交点);
当m=0时,方程是y=0(x≠±1),∴P的轨迹是x轴(除去(-1,0)和(1,0)两点);
当m>0时,方程可化为x2-
=1(x≠±1),∴P的轨迹是双曲线(除去项点)…12分.
| y |
| x+1 |
| y |
| x-1 |
∵k1•k2=m(m∈R),∴
| y |
| x+1 |
| y |
| x-1 |
所以所求轨迹方程是:mx2-y2=m(m∈R,x≠±1).…4分
(Ⅱ)由(Ⅰ)点P的轨迹方程为mx2-y2=m(m∈R,x≠±1),
当m<0且m≠-1时,方程可化为 x2+
| y2 |
| -m |
当m=-1时,方程x2+y2=1(x≠±1),∴P的轨迹是圆(除去与x的交点);
当m=0时,方程是y=0(x≠±1),∴P的轨迹是x轴(除去(-1,0)和(1,0)两点);
当m>0时,方程可化为x2-
| y2 |
| m |
点评:本题考查轨迹方程,考查分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
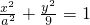 (a>0)与x轴的正半轴交于点P.点Q的坐标为(3,3),
(a>0)与x轴的正半轴交于点P.点Q的坐标为(3,3),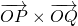 =6.
=6. 的直线交椭圆C于A、B两点,求△AOB的面积.
的直线交椭圆C于A、B两点,求△AOB的面积.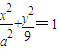 (a>0)与x轴的正半轴交于点P.点Q的坐标为(3,3),
(a>0)与x轴的正半轴交于点P.点Q的坐标为(3,3),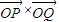 =6.
=6. 的直线交椭圆C于A、B两点,求△AOB的面积.
的直线交椭圆C于A、B两点,求△AOB的面积.