Question

设A={x|x²＋4x=0}，B={x|x²＋2（a＋1）x＋a²－1=0}，其中a∈R，如果A∩B=B，求实数a的取值范围.

Answer 1

解析：由题意易知B有四种情况，再对四种情况讨论转化为一元二次方程根的讨论.在进行运算时，容易疏漏B=的情况.若改为A∪B=A同样有BA.

答案：化简A={0，－4}，∵A∩B=B，∴BA.

（1）当B=时，Δ=4（a＋1）²－4（a²－1）＜0，解得a＜－1.?

（2）当B={0}或{4}，即BA时，Δ=4（a＋1）²－4（a²－1）=0，解得a=－1，此时B={0}，满足BA.

（3）当B={0，－4}时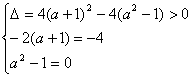，解得a=1.

综上所述，实数a的取值范围是a=1或a≤－1.