题目内容

在直三棱柱ABC－A1B1C1中，AA1＝AB＝AC＝4，∠BAC＝90°，D为侧面ABB1A1的中心，E为BC的中点

(1)求证：平面B1DE⊥侧面BCC1B1；

(2)求异面直线A1B与B1E所成的角；

(3)求点C1到面B1DE的距离．

答案：
解析：

　　解：(1)连接AE，因为AB＝AC，E为BC的中点，所以AEBC　　1分

　　又侧面底面ABC，因此AE侧面　　2分

　　AE　所以平面侧面　　4分

　　(2)取AE中点F，连接DF，则DF∥

　　所以BDF为异面直线与所成的角　　6分

　　在△BDF中，BD＝2，，

　　

　　求异面直线与所成的角　　8分

　　(3)过C1作B1E的垂线C1H，易知C1H＝　　12分


练习册系列答案
相关题目
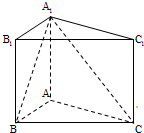精英家教网如图，在直三棱柱ABC-A1B1C1中，已知AB=AC，F为BB1上一点，BF=BC=2，FB1=1，D为BC中点，E为线段AD上不同于点A、D的任意一点．
（Ⅰ）证明：EF⊥FC1；
（Ⅱ）若AB=
2
，求DF与平面FA1C1所成的角．
如图，在直三棱柱ABC-A1B1C1中，底面ABC是等腰直角三角形，斜边AB=
2
a，侧棱AA1=2a，点D是AA1的中点，那么截面DBC与底面ABC所成二面角的大小是（　　）
在直三棱柱ABC-A1B1C1中，∠ACB=90°，AC=BC=AA1=1，D、E分别为棱AB、BC的中点，M为棱AA1上的点．
（1）证明：A1B1⊥C1D；
（2）当AM=
3
2
时，求二面角M-DE-A的大小．
如图，在直三棱柱ABC-A1B1C1中，AC=BC=AA1=2，∠ACB=90°，D、E分别为AC、AA1的中点．点F为
棱AB上的点．
（Ⅰ）当点F为AB的中点时．
（1）求证：EF⊥AC1；
（2）求点B1到平面DEF的距离．
（Ⅱ）若二面角A-DF-E的大小为
π
4
，求
AF
FB
的值．
精英家教网如图，在直三棱柱ABC-A1B1C1中，AB=1，AC=AA1=
3
，∠ABC=
π
3
．
（Ⅰ）证明：AB⊥A1C；
（Ⅱ）求二面角A-A1C-B的正弦值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网