题目内容
在锐角△ABC中，
，边a，b是方程
的两个实根．
求：（1）求角C的值；
（2）三角形面积S及边c的长．
解：（1）由已知
．∴
．
又A+B+C=π，∴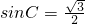
．在锐角△ABC中，C=60°．
（2）由韦达定理，
，∴
，
由余弦定理：c2=a2+b2-2abcosC=（a+b）2-3ab=12-6=6，∴
．
分析：（1）利用两角和正弦公式求得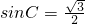，在锐角△ABC中，故有 C=60°．
（2）由韦达定理可得，由余弦定理：c2=a2+b2-2abcosC=（a+b）2-3ab，求得c的值．
点评：本题考查两角和正弦公式，余弦定理的应用，一元二次方程根与系数的关系，求出角C是解题的关键．
．∴．又A+B+C=π，∴
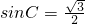．在锐角△ABC中，C=60°．（2）由韦达定理，
，∴，由余弦定理：c2=a2+b2-2abcosC=（a+b）2-3ab=12-6=6，∴
．分析：（1）利用两角和正弦公式求得
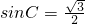，在锐角△ABC中，故有 C=60°．（2）由韦达定理可得
，由余弦定理：c2=a2+b2-2abcosC=（a+b）2-3ab，求得c的值．点评：本题考查两角和正弦公式，余弦定理的应用，一元二次方程根与系数的关系，求出角C是解题的关键．
练习册系列答案
相关题目