Question

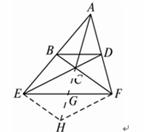
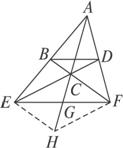
如图1-2-16，在四边形ABCD中，延长AD、BC交于F，延长AB、DC交于E，连结EF，且BD∥EF.求证:AC的延长线必平分EF.

图1-2-16

Answer 1

答案：
解析：

思路分析:本题可以利用平行四边形对角线特有的性质来证明线段相等，已知一组平行线，再做一组平行线EH∥BF，然后证明出CD∥HF即可. 证明：设AC延长后交EF于G，过E作BC的平行线交AG的延长线于H，连结HF， ∵EH∥BC,∴. 又∵BD∥EF,∴. ∴CD∥FH,即EC∥HF、CF∥EH. ∴四边形ECFH是平行四边形. ∴EG=GF,即AC的延长线必平分EF.