题目内容
【题目】过点![]() 作抛物线
作抛物线![]() 的两条切线, 切点分别为
的两条切线, 切点分别为![]() ,
, ![]() .
.
(1) 证明: ![]() 为定值;
为定值;
(2) 记△![]() 的外接圆的圆心为点
的外接圆的圆心为点![]() , 点
, 点![]() 是抛物线
是抛物线![]() 的焦点, 对任意实数
的焦点, 对任意实数![]() , 试判断以
, 试判断以![]() 为直径的圆是否恒过点
为直径的圆是否恒过点![]() ? 并说明理由.
? 并说明理由.
【答案】(I)详见解析;(II)详见解析.
【解析】试题分析:(Ⅰ)对![]() 求导,得到直线
求导,得到直线![]() 的斜率为
的斜率为![]() ,进一步得到直线
,进一步得到直线![]() 的方程为
的方程为![]() . 将点点
. 将点点![]() 代入直线
代入直线![]() 方程,整理得
方程,整理得![]() .
.
同理, ![]() . 又
. 又![]() , 所以
, 所以![]() 为定值.
为定值.
(Ⅱ)由题意可得)直线![]() 的垂直平分线方程为
的垂直平分线方程为![]() . ①
. ①
同理直线![]() 的垂直平分线方程为
的垂直平分线方程为![]() . ②
. ②
由①②解得点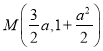 . 又 抛物线
. 又 抛物线![]() 的焦点为
的焦点为![]() 则
则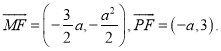 由
由![]() , 可得
, 可得![]() 所以以
所以以![]() 为直径的圆恒过点
为直径的圆恒过点![]()
试题解析:
(Ⅰ) 法1:由![]() ,得
,得![]() ,所以
,所以![]() .
.![]() 的斜率为
的斜率为![]() .
.
因为点![]() 和
和![]() 在抛物线
在抛物线![]() 上, 所以
上, 所以![]() ,
,![]() .
.
所以直线![]() 的方程为
的方程为![]() .
.
因为点![]() 在直线
在直线![]() 上,
上,
所以![]() ,即
,即![]() .
.
同理, ![]() .
.
所以![]() 是方程
是方程![]() 的两个根.
的两个根.
所以![]() .
.
又![]() ,
,
所以![]() 为定值.
为定值.
法2:设过点![]() 且与抛物线
且与抛物线![]() 相切的切线方程为
相切的切线方程为![]() ,
,
由![]() 消去
消去![]() 得
得![]() ,
,
由![]() , 化简得
, 化简得![]() .
.
所以![]() .
.
由![]() ,得
,得![]() ,所以
,所以![]() .
.
所以直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() .
.
所以![]() , 即
, 即![]() .
.
又![]() ,
,
所以![]() 为定值.
为定值.
(Ⅱ) 法1:直线![]() 的垂直平分线方程为
的垂直平分线方程为![]() ,
,
由于![]() ,
,![]() ,
,
所以直线![]() 的垂直平分线方程为
的垂直平分线方程为![]() . ①
. ①
同理直线![]() 的垂直平分线方程为
的垂直平分线方程为![]() . ②
. ②
由①②解得![]() ,
, ![]() ,
,
所以点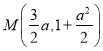 .
.
抛物线![]() 的焦点为
的焦点为![]() 则
则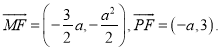
由于![]() ,
,
所以![]()
所以以![]() 为直径的圆恒过点
为直径的圆恒过点![]()
另法: 以![]() 为直径的圆的方程为
为直径的圆的方程为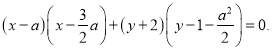
把点![]() 代入上方程,知点
代入上方程,知点![]() 的坐标是方程的解.
的坐标是方程的解.
所以以![]() 为直径的圆恒过点
为直径的圆恒过点![]()
法2:设点![]() 的坐标为
的坐标为![]() ,
,
则△![]() 的外接圆方程为
的外接圆方程为![]() ,
,
由于点![]() 在该圆上,
在该圆上,
则![]() ,
,
![]() .
.
两式相减得![]() , ①
, ①
由(Ⅰ)知![]() ,代入上式得
,代入上式得
![]() ,
,
当![]() 时, 得
时, 得![]() , ②
, ②
假设以![]() 为直径的圆恒过点
为直径的圆恒过点![]() ,则
,则![]() 即
即![]() ,
,
得![]() , ③
, ③
由②③解得![]() ,
,
所以点![]() .
.
当![]() 时, 则
时, 则![]() ,点
,点![]() .
.
所以以![]() 为直径的圆恒过点
为直径的圆恒过点![]()

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目