Question

【题目】已知函数

(1)讨论函数的单凋性；

(2)若存在使得对任意的不等式（其中e为自然对数的底数）都成立，求实数的取值范围．

Answer 1

【答案】（1）见解析；（2）.

【解析】试题分析：

(1)首先求解导函数，然后利用二次函数的性质结合导函数的分子分类讨论函数的单调区间即可；

(2)将问题进行等价转化，构造 ，结合函数 的性质求解实数 的取值范围即可.

试题解析：

（I） ，记

（i）当时，因为，所以，函数在上单调递增；

（ii）当时，因为，

所以，函数在上单调递增；

（iii）当时，由，解得，

所以函数在区间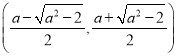上单调递减，

在区间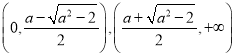上单调递增．

（II）由（I）知当时，函数在区间上单调递增，

所以当时，函数的最大值是，对任意的，

都存在，使得不等式成立，

等价于对任意的，不等式都成立，

即对任意的，不等式都成立，

记，由，

，

由得或,因为，所以，

①当时， ，且时， ，

时， ，所以，

所以时， 恒成立；

②当时， ，因为，所以，

此时单调递增，且，

所以时， 成立；

③当时， ， ，

所以存在使得，因此不恒成立．

综上， 的取值范围是．

另解（II）由（Ⅰ）知，当时，函数在区间上单调递增，

所以时，函数的最大值是，

对任意的，都存在，

使得不等式成立，

等价于对任意的，不等式都成立，

即对任意的，不等式都成立，

记，

由，且

∴对任意的，不等式都成立的必要条件为

又，

由得或

因为，所以，

当时， ，且时， ，

时， ，所以，

所以时， 恒成立；

②当时， ，因为，所以，

此时单调递增，且，

所以时， 成立．

综上， 的取值范围是．