题目内容
7.已知函数f(x)=$\frac{bx}{a{x}^{2}+1}$(b≠0,a>0).(1)判断f(x)的奇偶性;
(2)若f(1)=$\frac{1}{2}$,log3(4a-b)=$\frac{1}{2}$log24.
①求a,b的值.
②已知A,B是锐角三角形ABC的内角,试判断f(sinA)与f(cosB)的大小.
分析 (1)利用奇偶函数的定义判断f(-x)与f(x)的关系;
(2)已知得到关于a,b的方程解之;再利用函数的单调性,首先判断sinA与cosB的大小.再判断f(sinA)与f(cosB)的大小.
解答 解:(1)函数f(x)=$\frac{bx}{a{x}^{2}+1}$(b≠0,a>0).
f(-x)=$\frac{-bx}{a{x}^{2}+1}=-$f(x),所以函数f(x)为奇函数;
(2)若f(1)=$\frac{1}{2}$,log3(4a-b)=$\frac{1}{2}$log24.
则①$\frac{b}{a+1}=\frac{1}{2}$且4a-b=3,解得a=1,b=1;
②由①知,得到f(x)=$\frac{x}{{x}^{2}+1}$,f'(x)=$\frac{1-{x}^{2}}{{(x}^{2}+1)^{2}}$,由f'(x)>0得到-1<x<1时,f(x)为增函数,
又A,B是锐角三角形ABC的内角,所以A+B>$\frac{π}{2}$,即A>$\frac{π}{2}-B$,所以sinA>sin($\frac{π}{2}$-B)所以1>sinA>cosB>0,
所以f(sinA)>f(cosB).
点评 本题考查了函数的奇偶性以及单调性的运用;属于中档题.

练习册系列答案
相关题目
6.(1-$\frac{2}{{x}^{2}}$)(2+$\sqrt{x}$)6的展开式中,x项的系数是( )
| A. | 58 | B. | 62 | C. | 238 | D. | 242 |
15.若经过双曲线左焦点的直线与双曲线交于A,B两点,则把线段AB称为该双曲线的左焦点弦,双曲线C:$\frac{{x}^{2}}{4}$-y2=1长度为整数且不超过4的左焦点弦的条数为( )
| A. | 6 | B. | 7 | C. | 8 | D. | 10 |
12.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{3}=1(a>0)$的离心率为2,则其一条渐近线方程为( )
| A. | x-3y=0 | B. | $\sqrt{3}$x-y=0 | C. | x-$\sqrt{3}$y=0 | D. | 3x-y=0 |
19.设P为双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$右支上一点,O是坐标原点,以OP为直径的圆与直线$y=\frac{b}{a}x$的一个交点始终在第一象限,则双曲线离心率e的取值范围是( )
| A. | $({1,\sqrt{2}})$ | B. | $({1,\sqrt{2}}]$ | C. | $({\sqrt{2},+∞})$ | D. | $[{\sqrt{2},+∞})$ |
 在三棱锥A-BCD中,点A在BD上的射影为O,∠BAD=∠BCD=90°,AB=BC=2,AD=DC=2$\sqrt{3}$,AC=$\sqrt{6}$.
在三棱锥A-BCD中,点A在BD上的射影为O,∠BAD=∠BCD=90°,AB=BC=2,AD=DC=2$\sqrt{3}$,AC=$\sqrt{6}$.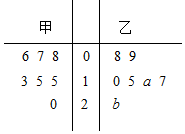 甲、乙两家快餐店对某日7个时段光顺的客人人数进行统计并绘制茎叶图如图所示(下面简称甲数据、乙数据),且乙数据的众数为17,甲数据的平均数比乙数据平均数少2.
甲、乙两家快餐店对某日7个时段光顺的客人人数进行统计并绘制茎叶图如图所示(下面简称甲数据、乙数据),且乙数据的众数为17,甲数据的平均数比乙数据平均数少2.