题目内容
设数列{an}是公差为d的等差数列,其前n项和为Sn.
已知a1=1,d=2,
①求当n∈N*时,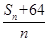 的最小值;
的最小值;
②当n∈N*时,求证: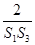 +
+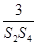 +…+
+…+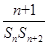 <
<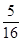 ;
;
已知a1=1,d=2,
①求当n∈N*时,
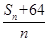 的最小值;
的最小值;②当n∈N*时,求证:
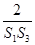 +
+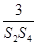 +…+
+…+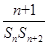 <
<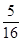 ;
;(1)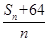 的最小值是16.
的最小值是16.
②证明:见解析。
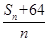 的最小值是16.
的最小值是16.②证明:见解析。
本试题主要是考查了数列的通项公式的求解以及数列求和的综合运用。
(1)根据已知条件,先得到通项公式,然后根据等差数列的前n项和公式得到最值。
(2)并结合第一问中的结论,得通项公式可知裂项,然后再求解和。
(1)①∵a1=1,d=2,
∴Sn=na1+ =n2,
=n2,
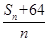 =n+
=n+ ≥2
≥2 =16,
=16,
当且仅当n= ,即n=8时,上式取等号,
,即n=8时,上式取等号,
故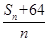 的最小值是16.
的最小值是16.
②证明:由①知Sn=n2,
当n∈N*时,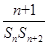
 ,
,
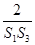 +
+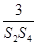 +…+
+…+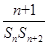
=
 +
+
 +…+
+…+


(1)根据已知条件,先得到通项公式,然后根据等差数列的前n项和公式得到最值。
(2)并结合第一问中的结论,得通项公式可知裂项,然后再求解和。
(1)①∵a1=1,d=2,
∴Sn=na1+
 =n2,
=n2,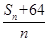 =n+
=n+ ≥2
≥2 =16,
=16,当且仅当n=
 ,即n=8时,上式取等号,
,即n=8时,上式取等号,故
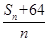 的最小值是16.
的最小值是16.②证明:由①知Sn=n2,
当n∈N*时,
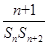
 ,
,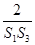 +
+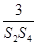 +…+
+…+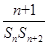
=

 +
+
 +…+
+…+



练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
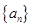 中,
中,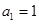 ,
, .
.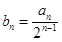 .证明:数列
.证明:数列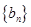 是等差数列;
是等差数列;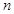 项和
项和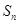 .
.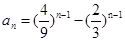 ,则数列{an}
,则数列{an} 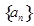 的前
的前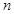 项和为
项和为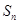 ,且
,且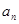 是
是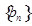 中,
中,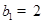 ,点
,点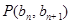 在直线
在直线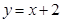 上.
上.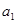 和
和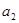 的值;
的值;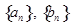 的通项
的通项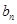 ;
;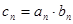 ,求数列
,求数列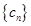 的前n项和
的前n项和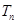 .
.  的前n项和为
的前n项和为 ,且
,且 .
.
 ,求数列
,求数列 的前
的前 项和
项和 .
.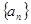 满足:
满足: .
. ,求数列
,求数列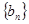 的前n项和
的前n项和 .
.